質量とエネルギーの等価性

質量欠損

原子核は陽子と中性子という核子からできているわけですが、不思議なことに原子核の質量は、陽子、中性子個々の質量の和より小さくなっています＊ トムソンの実験のような装置で質量を測ります。 閉じる 。

たとえば、陽子1個の質量は 1.0073u です。中性子1個の質量は 1.0087u です。これら2個ずつを合わせた質量は

　　2 × 1.0073 + 2 × 1.0087 = 2.0146 + 2.0174 = 4.0320 [u]

のはずですが、これらが結合したヘリウム原子核の質量は 4.0015u しかないのです。

このような差分のことを質量欠損といいます。陽子の質量を \(m_\rm{p}\)、中性子の質量を \(m_\rm{n}\)、原子番号\(Z\)、質量数\(A\)の原子核の質量を \(M\)、質量欠損 \(ΔM\) をとすると以下のように表せます。

＊ \((A-Z)\) の部分は \(N\) としても構いません。

また、上の例をこの式に当てはめると、
　0.0305 = 2 × 1.0073 + (4 - 2) × 1.0087 - 4.0015 [u]
となります。 閉じる

質量とエネルギーの等価性

1905年、アインシュタインは特殊相対性理論を提唱し、質量とエネルギーが等価であることを示しました。エネルギーを \(E\) [J]、静止している物体＊ 運動している場合には運動エネルギーも持っていることになります 閉じる の質量を \(m\) [kg]、真空中での光速を \(c\) [m/s] としたときに以下のように表される理論です＊ 導出方法は大学で学びます 閉じる 。

結合エネルギー

上式の意味は \(m\) の質量を持つ物体は \(mc^2\) のエネルギーを持つということです。\(ΔM\) であれば \(ΔMc^2\) のエネルギーということです。実はこのエネルギーは核子が結びついて原子核になるときに放出されたエネルギーなのです＊ γ線などとして放出されます 閉じる 。あるいは原子核をバラバラに引きはがすときに必要なエネルギーなのです＊ 核子同士は核力で引きつけ合ってます 閉じる 。それが質量欠損として現れるのです。このエネルギーを結合エネルギーといいます。＊ 質量欠損や結合エネルギーはすべての物体の結合に備わるものなのですが、測定可能なほど顕著に現れるのが核子同士の結合です。核力というものが強大だからです。

また、質量欠損が存在するということは質量保存の法則が成り立っていないということになりますが、質量がエネルギーと等価であるということなら結局エネルギー保存の法則が成り立っているということになります。

さらに、上で例に挙げたヘリウム原子核の結合エネルギーを割り出してみますと、
質量欠損が 0.0305u で、(u =) 1.66×10^-27kg を掛けると 0.05063×10^-27kg で、これに真空中の高速 3.00×10⁸m/s の2乗を掛けると 0.45567×10^-27×10¹⁶ = 4.56×10^-12 [J] となります。[eV] に変換すれば 1.6×10^-19 で割って、2.85×10⁷eV となり、これをメガで表すと、28.5MeV となります。

あと、くれぐれも原子核が結合エネルギーというものを抱えてるわけではないことに注意してください。むしろ逆です。原子核は結合エネルギー分、エネルギーが小さくなっているのです。 閉じる

核子1個当たりの結合エネルギー

核子の多い原子核ほど結合エネルギーは大きいのですが、それを核子の数（=質量数）で割った値は各々の核子がどれだけ強固に結びついているかを表していることになります。核子1個当たりの結合エネルギー \({\large\frac{ΔMc^2}{A}}\) を以下に示します。

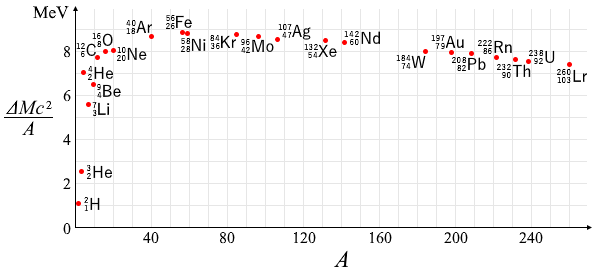
\(\ce{^{56}_{26}Fe}\) が最も強くなってます＊ 厳密には \(\ce{^{62}_{28}Ni}\) が最強らしいです 閉じる 。たしかに鉄は地球に豊富に存在します。\(\ce{^{4}_{2}He}\) も質量数が小さい割には強いです＊ グラフをよく見ていただくと、上の＊の中で計算した値 28.5MeV を質量数4で割った値、約7.1MeV となってます。 閉じる 。

核子たちは核力で引きつけ合っていて、だんご状に集まるとその効率が上がりますが、核力は近距離でしかはたらかないため、たくさん集まり過ぎて距離の遠い核子ができてしまうと効率が悪化して、1個当たりの結合エネルギーは低下してしまいます。

＊ 電子と原子核の間にも引力がはたらいているので結合エネルギーがあるとみなせますが、原子核内の核子の間の結合エネルギーよりはるかに小さいです。 閉じる