弧度法
rad
高校数学、高校物理では角度の単位として、ラジアンというものをよく用います ラジアン radian の語源はおそらく radiate（放射状に伸びる） radiant（光を放つ） radius（半径） あたりと共通と思われます。 。[rad] と表記します。この角度の測り方を弧度法（こどほう）といいます。今まで使ってきた [°] で表す測り方の名前は度数法です。
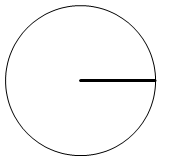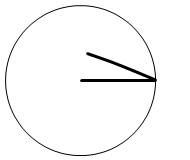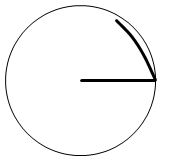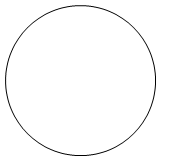ラジアンは円における半径と弧の比によって決められている単位です。
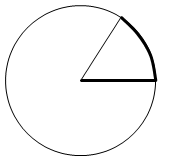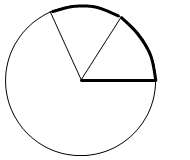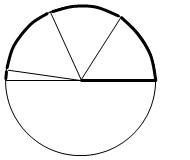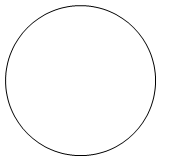
弧の長さが半径と同じになるような扇型の中心角を基本単位としていて、それが 1rad です。
この角度は円の大きさによりません。小さい円においても大きい円においても同じ大きさです。
省略可
この角度は半径の長さと弧の長さの比であるともいえ、比であるならば単位が無い \({\large\frac{弧の長さの単位}{半径の長さの単位}}\) = \({\large\frac{[m]}{[m]}}\) = 1（無次元数）。単位の演算参照。 、とみなすことができ、その単位 [rad] を省略することがあります。省略できるので何かと合理的で便利です。
ただ単に \(θ\) などと書かれている場合は \(θ\) [rad] のことです。弧度法でなく度数法で角度を示すときは [°] を絶対付けなければなりません。
1rad ≒ 57.3°
弧と半径が同じになるとき、その角度は度数法でいうと 約57.3° です。1rad ≒ 57.3° です。
そして 1rad を約3.14倍すると 180° になります。57.3° × 3.14 ≒ 180° です。半円周の長さというのは \(πr\) ですが、これは半径 \(r\) を \(π\)(3.14)倍したものでありますが、1rad のときの弧の長さは半径と同じであるので、1rad のときの弧の長さ \(r\) を \(π\)(3.14)倍したものともいえます。
1rad ≒ 57.3° であり 3.14rad ≒ 180° です。ラジアンという単位がしっくりこない方は、「 rad は 57.3 という単なる数値、\(π\) というのは 3.14 という単なる数値。」ととりあえず覚えてください。
\(π\) rad = 180° 、2\(π\) rad = 360° 、\({\large\frac{\pi}{2}}\)rad = 90° 、\({\large\frac{\pi}{3}}\)rad = 60° 、\({\large\frac{\pi}{4}}\)rad = 45° です。