ベクトル
ベクトルとは
ベクトルとは、大きさに向きを付加した量です。大きさだけを表す量をスカラーといいます。＊ベクトル量、スカラー量、ということもあります。
閉じる
りんご5個、身長160cm、速さ …… スカラー
北西へ10km、-10m/s2、速度 …… ベクトル
高校物理では、「速さ」はスカラーで「速度」はベクトル、と使い分けています。
ベクトルを量記号で表すときは、文字の上に矢印を付けます。
\(\vec{a}\) 、\(\vec{x}\) 、\(\vec{A}\)
単純に足せない
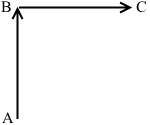A市から北へ10kmのB市に行き、次に、B市から東へ10kmのC市に行ったとき、走行距離は20kmかもしれませんが、A市とC市との距離は (10×\(\sqrt{2}\) ≒) 約14.1km です＊
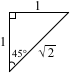直角２等辺三角形の辺の比は 1:1:\(\sqrt{2}\) です。
\(\sqrt{2}\) は約1.4142 です。
閉じる。
右に7m行って、左に10m行って、右に1m行った場合、走行距離（スカラー）は18mですが、位置関係（ベクトル）は、左に2m、です。ベクトルでは始点と終点が重要になります。途中経路は関係ありません。
あいまい
商品の値段はスカラーのはずですが、昨今、激安携帯ショップなどで「一括0円、キャシュバック3万円！」などという売り方をしていたりしますので、この場合の値段は-30000円と考えることができ、これはもはやベクトル、とみなすことができます。
燃料タンクにおいて、燃料を補給したときは+10リットルで、燃料を消費したときは-10リットル、と考えればこれはベクトルです。
子供にりんごを1個ずつ配って、余ったら+3個で、足りなかったら-3個、と考えればこれもベクトルです。
1次元（数直線。あるいは増減を考えるとき。）で量を考えるときは、スカラーともベクトルとも考えられる場合があるので注意が必要です。特に数式を立てるときは要注意です。極論をいいますと、全ての量はベクトルであって、たまたま向きを無視できるときだけスカラー、と考えることができます。
ベクトルの図示
ベクトルを図示するときは矢印で表現します。長さがベクトルの大きさを表し、矢印の向きがベクトルの向きを表します。ベクトルの大きさがわかってないときは長さを正確に図示することはできませんが、向きについては（高校物理では）わかっていることが多いのでなるべく正確に描いてください。
ベクトルを 1.4倍すると、長さが 1.4倍になります。向きは変わりません。
ベクトルに -1 を掛けると、長さは変わらず、向きが逆になります。
加法と減法
ベクトルとベクトルは平行四辺形の法則によって合成することができます。ベクトルの起点をそろえて平行四辺形を描くと、その対角線が合成されたベクトルになります。青矢印+青矢印=赤矢印 です。（ベクトルの加法）
あるいは三角形を作ることによって合成することができます。同じことです。
加える順番を変えても結果は同じです。
\(\color{#00f}{\vec{a}}\) + \(\color{#0c0}{\vec{b}}\) + \(\color{#c0c}{\vec{c}}\) = \(\color{#0c0}{\vec{b}}\) + \(\color{#c0c}{\vec{c}}\) + \(\color{#00f}{\vec{a}}\) です。
ベクトルからベクトルを引くときは、基準となるベクトルの先端から対象となるベクトルの先端へ矢印を引きます。（ベクトルの減法）
これは基準ベクトルを反対向きにしてから合成するのと同じことです。
\(\vec{a}\) - \(\vec{b}\) = \(\vec{a}\) + (-\(\vec{b}\)) です。
直交座標の各成分への分解
ベクトルは平行四辺形の法則によって分解することができます。
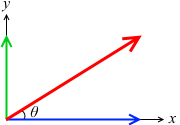高校物理では直交座標の各成分へ分解することが多いです。
\(|\color{#f00}{\vec{R}}|\) = R のとき、
\(|\color{#00f}{\vec{R_x}}|\) = Rx = Rcosθ 、\(|\color{#0c0}{\vec{R_y}}|\) = Ry = Rsinθ
R = \(\sqrt{\left(R\cos\theta\right)^2+\left(R\sin\theta\right)^2}\)
tanθ = \(\large{\frac{R_y}{R_x}}\)
という関係があります。