力
力とは
物体が変形したり動く速度が変わったりするのは、物体に力がはたらくからです。何も力がはたらかなければ変形もしないし、速度も変わりません。また、変形しなくても、石が地面に置かれて静止している時でも、石には重力という力がたらいています。この世の全ての物に力は関係していて、物事の現象の根源を探るには力のはたらきについて考えなければなりません。物理は力について考える学問といえるかもしれません。
力の種類には、重力、人間の筋肉による力、ひもが物を引っ張る張力、物を引きずる時に感じる摩擦力、水の中の物体を持ち上げようとする浮力、ばねによる弾性力、荷電粒子の間にはたらく静電気力（クーロン力）、磁石同士が引き合う磁気力、床から押し返される垂直抗力などがあります。
このように力にはいろいろな名前が付いていますが、そのどれもが元を辿ると重力か電磁気力の2種類の力に行き着きます＊他に”強い力””弱い力”というものもあり、厳密にいうと全部で4種類あります。これら4種類の力の根源を辿る研究もあり、大統一理論、超ひも理論などと呼ばれています。
閉じる。人間の筋肉による力も、脳内で発生した電気信号を神経細胞が腕の筋肉に伝え、筋肉細胞を構成する分子たちが電気をやりとりして、筋肉を縮めたり伸ばしたりするものです。ロープにはたらく張力も、ロープを構成する綿や化学繊維の分子が分子間力によって、外から引っ張られる力に対抗している力です。分子間力の元は電磁気力です。摩擦力と浮力の元は重力ですし、弾性力の元は電磁気力です。
いろいろな力があると言っても、おおもとは2種類であり、その2種類の力をさまざまな場面によって張力、摩擦力、浮力、弾性力などと名前を付けて呼んでいるわけです。高校物理ではこれら張力、摩擦力、浮力、弾性力などについて個別に学んでいきます。
力の表し方
力を表すとき、大きさだけでなく、向きも表さなければなりません。つまりベクトルです。
記号で表すときは \(\vec{F}\) という風に上に矢印を付けます。 矢印無しにするとそれは大きさだけを表していることになります。\(\vec{F}\) の大きさが \(F\) です。＊F は force（力）から。
物理量を表す記号を量記号といいます。どのアルファベットを用いるかは慣習でだいたい決まっています。厳密ではありません。
[N] や [m] や [kg] などの単位記号は厳密に決まっています。
閉じる
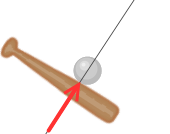
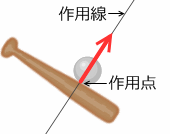図で示すときは、矢印の長さで力の大きさを示し、矢印の向きで力の向きを示します。さらに、力が作用する点を示すことが重要で、その点が矢印の始点となるように図示します。この点を作用点といい、作用点を通り力の方向に引いた直線を作用線といいます。力の大きさ、向き、作用点（もしくは作用線）を力の三要素といいます。
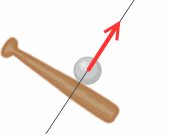上図の赤い矢印を少しずらして左図のように図示することもあります。力は作用線上なら移動してもそのはたらきは変わりません。実は作用点が大事なのではなく作用線が大事なのです。
矢印の大きさと向きは変えてはいけません。
たとえばこのような場合、
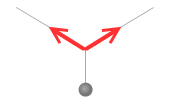このように移動させたりします。物理では考えやすいように矢印を作用線に沿って移動させることがよくあります。
＊
このように描いたり、
このように描いたりすることはあまりありません。
矢印の先を作用点に合わせることはほとんどありません。
力を描くときは矢印の起点を作用点に合わせることが多いです。押すときでも引っ張るときでもそうです。
閉じる
引力と斥力
互いに引き合う力を引力といい、互いに遠ざけようとする力を斥力（せきりょく）といいます。
力の単位
力の単位には [N] ニュートン が用いられます。あの有名なニュートンからきています。1.0N は質量 1.0kg の物体に 1.0m/s² の加速度を生じさせるような力と定義されています。何のことかわからないと思いますが、後で習う運動方程式というものから導き出されるもので、物体に力を加えると速度が増すという ma = F という式において質量 m = 1.0 [kg]、加速度 a = 1.0 [m/s²] のときの力が F = 1.0 [N] と定められています。
ここで、「 1.0kg の物体に → 1.0m/s² の加速度を生じさせるような力が → 1.0N である 」ということを頭において、次の説明を読んでください。
地球は重力という力によって地球上のあらゆる物体を引っ張っています。そしてそのときの加速度は 9.8m/s² です。
ということは、1.0kg の物体にかかる重力という力の大きさは 9.8N ということになります。（ 2.0kg の物体にかかる重力でしたら 2×9.8 [N] です。2.0kg の物体に 9.8m/s² の加速度を生じさせるのですから。）
では、1.0N という力の大きさは重力でいうとどのくらいでしょう。
1.0kg の物体に → 9.8m/s² の加速度を生じさせるのが → 9.8N
●kg の物体に → 9.8m/s² の加速度を生じさせるのが → 1.0N
●は \(\large{\frac{1.0}{9.8}}\) kg です。計算すると 約0.102kg です。約0.102 kg ほどの物体を重力が引っ張るときの力が 1.0N ということです。感覚的にいうと、1.0N という力の大きさは、手のひらにみかんを置いたときに感じるくらいの力、ということです。
これらのことを『自由落下運動』項で示した \(g\) (=9.8 m/s²) という記号を使って表してみますと、
1.0kg の物体にかかる重力 = 9.8 [N] = \(g\) [N]
2.0kg の物体にかかる重力 = 2×9.8 [N] = 2.0\(g\) [N]
0.102kg の物体にかかる重力 = 1.0 [N] = 0.102×9.8 [N] = 0.102\(g\) [N]
\(m\) [kg] の物体にかかる重力 = \(m\)×9.8 [N] = \(mg\) [N]
と表すことができます。
ややこしくて混乱すると思うのでこの説明は何度も読み返してください。昔は kg重（きろぐらむじゅう）という分かりやすい単位があったのですがこの単位は使用されなくなったようです。