ボイル⋅シャルルの法則の補足
気体の圧力
本項で説明した気体の圧力について、もう少し説明します。
ピストン付きシリンダーに何らかの気体が入れられているとします。シリンダーの断面積を \(S\) 、内部の圧力を \(p\) 、ピストンには重さが無く、大気圧を \(p_0\) とします。
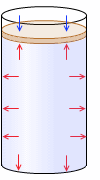内部の気体がピストンを押し上げる力は \(pS\)
圧力が \(p = {\large\frac{F}{S}}\) なのだから \(F = pS\) です
、大気がピストンを押し下げる力は \(p_0S\) です。このときピストンが静止している（つり合っている）とすると、\(pS = p_0S\) です。すなわち、
\(p = p_0\)
です。内部と外部の気体の圧力は等しいということです。当たり前ですが。
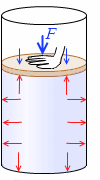手でピストンを押し下げてつり合ったとします。この時の手の力を \(F\) とすると、つり合いの式は \(pS = p_0S + F\) です。すなわち、シリンダー内の気体の圧力は、
\(p = p_0 + {\large\frac{F}{S}}\)
です。
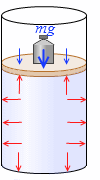手で押すのではなく、おもりが乗っていてつり合ったとします。おもりの質量を \(m\) 、重力加速度を \(g\) とすると、つり合いの式は \(pS = p_0S + mg\) です。すなわち、シリンダー内の気体の圧力は、
\(p = p_0 + {\large\frac{mg}{S}}\)
です。
温度を一定に保つ方法
ボイルの法則は温度一定のもとで成り立つ法則ですが、その時、温度を一定に保つのに、温度センサーや加熱器を使ったりする必要はありません。シリンダーが熱を伝える材質でできていれば良いのです。そのようなシリンダーを用いて熱が伝わるのを待ちながらゆっくり変化させれば良いのです。そうすれば自動的に外気と同じ温度が保たれます。ですので、ボイルの法則を確かめる実験をするときは、激しくピストンを動かしてはいけません。等温変化に関する実験を行うときはピストンをゆっくり動かさなければなりません。
等温変化における温度単位
ボイルの法則を含む等温変化においては、温度単位が絶対温度であるかセ氏温度であるかを気にする必要はありません。どっちみち温度は一定なのですから。しかしその他のシャルルの法則などについては、絶対温度であるかセ氏温度であるかを気にしなければなりません。
温度でなく温度差が問題であるなら、絶対温度であるかセ氏温度であるかを気にする必要はありません。
シャルルが実験で導き出した式
シャルルが実験で導き出した \(V = V_0({\small 1} + {\large\frac{1}{273}}t\)) という式の意味は、セ氏温度 \(t\) が 1℃ 下がるごとに、0℃ のときの体積 \(V_0\) の 1/273 ずつ体積が減っていくという意味です。
\(t\) = -1 ℃ のとき \(V = V_0\{{\small 1} + {\large\frac{1}{273}}{\small(-1)}\} = {\large\frac{272}{273}}\)\(V_0\)
\(t\) = -273 ℃ のとき \(V = V_0\{{\small 1} + {\large\frac{1}{273}}{\small(-273)}\} = 0\)
です。セ氏温度が -273℃ だと、体積 \(V\) が 0 になるのです 理想気体での話です 。体積はこれ以上小さくなれないので温度もここまでが限界で、この温度が絶対零度です。
ボイルの法則とシャルルの法則の組み合わせ
ボイルの法則とシャルルの法則がなぜ組み合わせることができるのか、説明します。
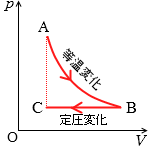一定量の気体を左図のように変化させることを考えます。縦軸が圧力で横軸が体積を表します。状態Aから状態Bの変化は等温変化で、状態Bから状態Cは定圧変化です。
状態Aから状態Bの変化は等温変化なのでボイルの法則が成り立ち、
\(p_{\rm A}V_{\rm A} = p_{\rm B}V_{\rm B}\) ……①
です。状態Bから状態Cは定圧変化なのでシャルルの法則が成り立ち、
\({\large\frac{V_{\rm B}}{T_{\rm B}}} = {\large\frac{V_{\rm C}}{T_{\rm C}}}\)
∴ \(V_{\rm B} = {\large\frac{V_{\rm C}T_{\rm B}}{T_{\rm C}}}\)
です。これを①式に代入しますと、
\(p_{\rm A}V_{\rm A} = p_{\rm B}{\large\frac{V_{\rm C}T_{\rm B}}{T_{\rm C}}}\)
です。また、状態Aから状態Bの変化は等温変化なので \(T_{\rm A} = T_{\rm B}\) 、
状態Bから状態Cの変化は定圧変化なので \(p_{\rm B} = p_{\rm C}\) 、
これらを上式に代入すると、
\(p_{\rm A}V_{\rm A} = {\color{#080}{p_{\rm C}}}{\large\frac{V_{\rm C}{\color{#b00}{T_{\rm A}}}}{T_{\rm C}}}\)
∴ \({\large\frac{p_{\rm A}V_{\rm A}}{T_{\rm A}}} = {\large\frac{p_{\rm C}V_{\rm C}}{T_{\rm C}}}\)
となり、ボイル⋅シャルルの法則が導かれます。