力のつり合い

力のつり合い

物体に複数の力が作用しているのに、物体が動かない場合、これらの力はつり合っているといいます。これは複数の力の合力が 0 になっているからで、この現象を力のつり合いといいます。

また、物体が動かないというような場合だけでなく、等速度運動しているような場合も、力がつり合っているといいます。自動車でいうとアクセルとブレーキを同時に踏んで、速度が一定であるような場合です。アクセルによる前に進む力とそれを邪魔するブレーキの力がつり合いながら、一定の速度で進んでいる状態です。一定でなく、速度が上がるようであればアクセルの勝ち、速度が下がるようであればブレーキの勝ちで、このような場合はつり合っているとはいえません。後で慣性の法則というものを習うとちゃんと理解できると思います。

要するに、複数の力がはたらいているのに物体の運動状態が変化しないような場合、力がつり合っている、と物理では表現するのです。

2力のつり合い

2つの力がつり合うときの条件を考えてみますと、まず向きが逆で大きさが等しいということが思い浮かびます。ベクトル式で書くと \(\vec{F_1} = -\vec{F_2}\)、または \(\vec{F_1} + \vec{F_2} = 0\) です。

しかしもう一つ条件がありまして、それは同一作用線上にあるということです。同一作用線上にないと物体が動いてしまう（運動の状態が変化してしまう）ので力がつり合っているといえなくなってしまいます。左図の場合では、始めは同一作用線上になく、力はつり合っているとはいえませんが、物体が回転していずれ同一作用線上に力が乗ってつり合うことになります。

3力のつり合い

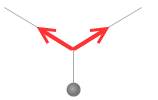左図は力のページで示した図ですが、この図では2つの力しか示していませんでした。

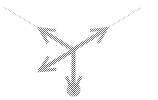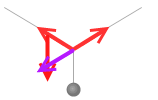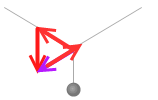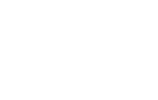
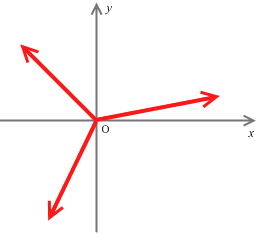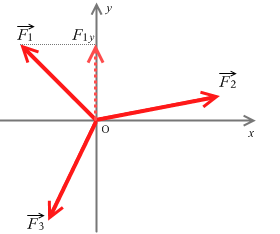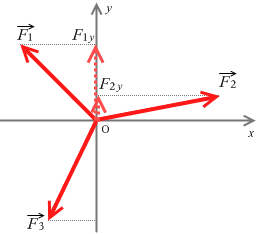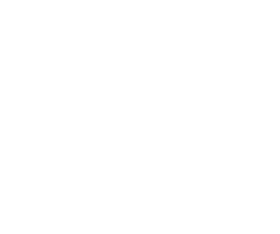
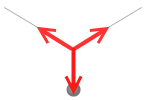しかし、本当は下向きの重力があるので左図のようになります。このとき物体が動かなければ3力はつり合っているということになります。

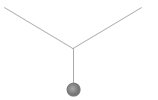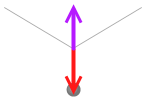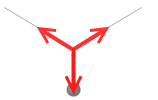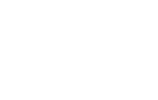上側の2つの力の合力は上向きの紫色矢印の力となり、この力が下向きの力とつり合っているということです。ベクトル式で書くと \(\vec{F_1} + \vec{F_2} = -\vec{F_3}\) 、または \(\vec{F_1} + \vec{F_2} + \vec{F_3} = 0\) です。

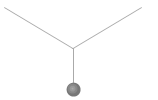そしてつり合っているときというのは3つの力の作用線が1点で交わるときです。この点を作用点といいます。

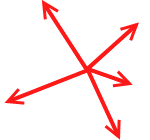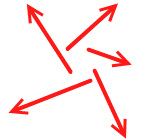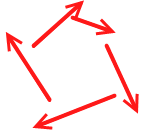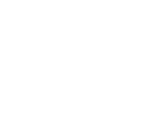
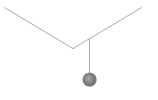作用線が1点で交わらないような場合、例えば左図のような場合や、

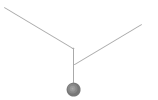左図のような場合などは、物体が動いてしまうので力がつり合っているとはいえなくなってしまいます。

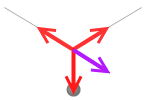また紫色矢印の作り方は、別の考え方として、

右上向きの力と下向きの力の合力が右下向きの紫色の力で、その力が左上向きの力とつり合っていると考えてもいいし、

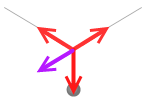左上向きの力と下向きの力の合力が左下向きの紫色の力で、その力が右上向きの力とつり合っていると考えてもいいです。

またこれらのことは矢印を平行移動させていくと閉じた三角形ができることを意味します。「閉じた」という意味は各ベクトルの終点を隣のベクトルの始点に合わせるときれいに数珠つなぎ＊じゅずつなぎ … ひとつなぎにすること閉じるになって隙間なくひと回りするという意味です。

4つの力がつり合っているときであれば、平行移動させていくと閉じた四角形ができます。

各成分の和も 0

さらに、力がつり合っているときはそれらの力の x成分だけ、y成分だけを抜き出して足し合わせると 0 になります。

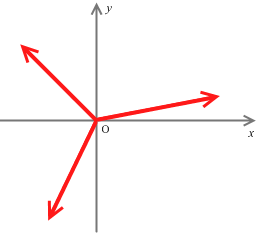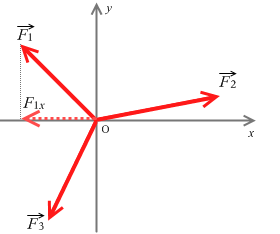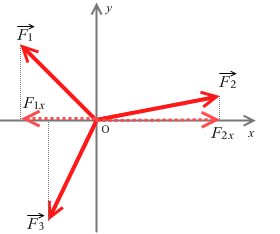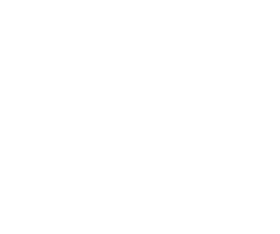左図は x成分だけを抜き出したところです。力がつり合っているときはそれらを足し合わせると 0 になります。式で書くと \(F_1x + F_2x + F_3x = 0\) です。

左図は y成分だけを抜き出したところです。力がつり合っているときはそれらを足し合わせると 0 になります。式で書くと \(F_1y + F_2y + F_3y = 0\) です。

n個の力のつり合い

n個の力がつり合っているときというのは、

　　それらの力の作用線は1点で交わり、

　　\(\vec{F_1} + \vec{F_2} + \vec{F_3} + \cdots + \vec{F_n} = 0\)

となっています。

上式は成分で表すと、

　　\(F_1x + F_2x + F_3x + \cdots + F_nx = 0\)

　　\(F_1y + F_2y + F_3y + \cdots + F_ny = 0\)

とも表現できます。

また、それらの力を表すベクトルを平行移動＊通常、力は作用線上以外は移動させてはいけないのですが、いまは「閉じたn角形」ができるかどうかだけを考えているので特別です。
n角形を作ったときには、作用線は1点で交わっていません。閉じるさせて数珠つなぎにすると閉じたn角形ができます。

『剛体にはたらく力のつり合い』項、『慣性の法則』項もご参照ください。