ボイル⋅シャルルの法則
気体の圧力
気体を容器に閉じ込めると、気体分子は容器内を激しく飛び回り、壁に衝突します。容器内の気体分子はどの分子も同じ力で壁に衝突します。容器の真ん中付近の分子だけが勢いが強くて、端の方の分子は勢いが弱いというようなことはありません。パスカルの原理がはたらいていて、どこも一様です
水圧について考えるときは、その高さについて考慮しましたが、気体の圧力を考える場合は、どこもかしこも一様、とみなします。
大気圧について考えるときは高さを考慮する場合があります。
。
気体の圧力というのは、面におよぼす単位面積当たりの力のことであります。面積 \(S\) [m2] の面に垂直に加わる力の大きさが \(F\) [N] であるときに、圧力 \(p\) [Pa] は、
\(p = {\large\frac{F}{S}}\)
と表されます。
 気体の圧力の根源は、分子
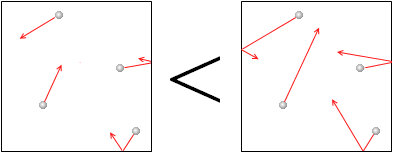
気体の圧力の根源は、分子 の熱運動であり、その運動が激しいほど、つまり、温度が高いほど、圧力は大きくなります。
の熱運動であり、その運動が激しいほど、つまり、温度が高いほど、圧力は大きくなります。
(左図の赤矢印の長さは熱運動の激しさを表現しています。)
 また、分子
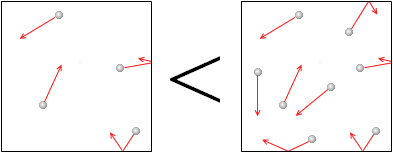
また、分子 の数が多いほど気体の圧力は大きくなります。壁に当たる分子の数が増えるからです。別の表現をしますと、同じ分子の数であれば体積が小さいほど気体の圧力が大きくなります。単位体積当たりの分子の数が多くなるほど気体の圧力は大きくなるのです。
の数が多いほど気体の圧力は大きくなります。壁に当たる分子の数が増えるからです。別の表現をしますと、同じ分子の数であれば体積が小さいほど気体の圧力が大きくなります。単位体積当たりの分子の数が多くなるほど気体の圧力は大きくなるのです。
気圧
100Pa を 1hPa(いちへくとぱすかる)といいます。h(へくと)というのは 100 という意味です。この単位は天気予報で大気圧を表すときなどに使われます。海面での大気圧の標準値は 1013hPa です。これを 1気圧、あるいは 1atm(いちあとむ) 大気 atmosphere から といいます。
1 気圧 = 1 atm = 1013 hPa = 101300 Pa = 1.013×105 Pa
です。
ボイルの法則
 一定量(左図では分子
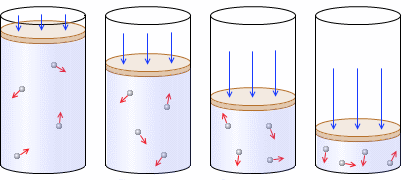
一定量(左図では分子 4個)の気体をピストン付きシリンダーの中に入れ、温度を一定に保ちながら、ピストンを押して気体を圧縮して体積を小さくしていくと、圧力は大きくなっていきます。体積を1/2、1/3、1/4と圧縮していくと圧力が2倍、3倍、4倍になっていきます。体積が小さくなると分子の壁への衝突回数が増えるからです。
4個)の気体をピストン付きシリンダーの中に入れ、温度を一定に保ちながら、ピストンを押して気体を圧縮して体積を小さくしていくと、圧力は大きくなっていきます。体積を1/2、1/3、1/4と圧縮していくと圧力が2倍、3倍、4倍になっていきます。体積が小さくなると分子の壁への衝突回数が増えるからです。
温度が一定のとき、気体の圧力 \(p\) [Pa] は体積 \(V\) [m3] に反比例するのです。これをボイルの法則といいます
17世紀のアイルランドの物理学者、ロバート⋅ボイル Robert Boyle が発見しました。
お湯を沸かすときのボイルは boil 。
。
ボイルの法則
温度と質量が一定のとき、気体の圧力 \(p\) は体積 \(V\) に反比例する
\(\boldsymbol{pV = k}\)(一定)
\(p_1V_1 = p_2V_2\) などと表現することもあります。
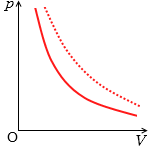 ボイルの法則をグラフで表わすと左図のようになります。反比例のグラフです。この曲線を等温曲線(等温線)といいます。温度が高かったり質量(=分子の数)が大きかったりすると、グラフの曲線は点線の位置に移動します。これはボイルの法則の式における \(k\) のことを指します。温度や質量が大きくなると \(k\) が大きくなり、グラフの曲線は原点から遠ざかります。\(k\) は比例定数の \(k\) ですが、このような意味があります。
ボイルの法則をグラフで表わすと左図のようになります。反比例のグラフです。この曲線を等温曲線(等温線)といいます。温度が高かったり質量(=分子の数)が大きかったりすると、グラフの曲線は点線の位置に移動します。これはボイルの法則の式における \(k\) のことを指します。温度や質量が大きくなると \(k\) が大きくなり、グラフの曲線は原点から遠ざかります。\(k\) は比例定数の \(k\) ですが、このような意味があります。
ボイルの法則のように、気体の温度が一定で圧力や体積が変化することを等温変化といいます。
シャルルの法則
 一定量(左図では分子
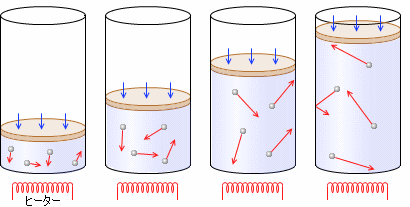
一定量(左図では分子 4個)の気体をピストン付きシリンダーの中に入れ、圧力を一定に保ちながら、気体を加熱していくと、体積は大きくなっていきます。上で説明したように、温度が上がると分子が壁に勢いよく当たり、衝突回数も増えて、圧力が上がります。ピストンには重さが無く、かつ自由に動けるようにしておく(つまり、シリンダー内部の圧力と外部の圧力が等しくなるようにしておく)と、圧力が高まった内部の気体がピストンを押し、外部の気体の圧力とつり合うまでピストンを持ち上げます。
4個)の気体をピストン付きシリンダーの中に入れ、圧力を一定に保ちながら、気体を加熱していくと、体積は大きくなっていきます。上で説明したように、温度が上がると分子が壁に勢いよく当たり、衝突回数も増えて、圧力が上がります。ピストンには重さが無く、かつ自由に動けるようにしておく(つまり、シリンダー内部の圧力と外部の圧力が等しくなるようにしておく)と、圧力が高まった内部の気体がピストンを押し、外部の気体の圧力とつり合うまでピストンを持ち上げます。
圧力が一定のとき、気体の絶対温度 \(T\) [K] は体積 \(V\) [m3] に比例するのです。これをシャルルの法則といいます 18世紀のフランスの物理学者ジャック・シャルルが発見しました 。
シャルルの法則
圧力と質量が一定のとき、気体の絶対温度 \(T\) は体積 \(V\) に比例する
\(\boldsymbol{{\large\frac{V}{T}} = k}\)(一定)
\({\large\frac{V_1}{T_1}} = {\large\frac{V_2}{T_2}}\) などと表現することもあります。
実際にシャルルが実験で導き出した式は、一定の圧力において 0℃ のときの気体の体積を \(V_0\) [m3]、セルシウス温度を \(t\) [℃]、そのときの体積を \(V\) [m3] とし、
シャルルの法則(セルシウス温度)
\(\boldsymbol{V = V_0(1 + {\large\frac{1}{273}}t)}\)
というものでした。この式に絶対温度とセルシウス温度の関係式 \(T = t + 273\) を代入すると、
\(V = V_0(1 + {\large\frac{1}{273}}t\)) 273倍して
\(= {\large\frac{V_0}{273}}(273 + t\)) \(t\) を代入
\(= {\large\frac{V_0}{273}}(273 + T - 273)\)
\(= {\large\frac{V_0}{273}}T\)
∴ \({\large\frac{V}{T}} = {\large\frac{V_0}{273}}\) (\({\large\frac{V_0}{273}}\) は定数、つまり \(k\) とおける)
となり、絶対温度でのシャルルの法則の式が導き出されます。
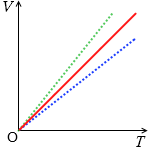 シャルルの法則をグラフで表わすと左図のようになります。比例のグラフです。圧力が高いとグラフの曲線は温度軸に近づきます。質量(=分子の数)が大きいとグラフの曲線は体積軸に近づきます。
シャルルの法則をグラフで表わすと左図のようになります。比例のグラフです。圧力が高いとグラフの曲線は温度軸に近づきます。質量(=分子の数)が大きいとグラフの曲線は体積軸に近づきます。
シャルルの法則のように、気体の圧力が一定で温度や体積が変化することを定圧変化といいます。
ボイル⋅シャルルの法則
ボイルの法則 \(pV = k\) と、シャルルの法則 \({\large\frac{V}{T}} = k\) は組み合わせることができます。ボイル⋅シャルルの法則といいます。
ボイル⋅シャルルの法則
質量が一定のとき、気体の体積 \(\boldsymbol{V}\) は、圧力 \(\boldsymbol{p}\) に反比例し、絶対温度 \(\boldsymbol{T}\) に比例する
\(\boldsymbol{{\large\frac{pV}{T}} = k}\)(一定)
\({\large\frac{p_1V_1}{T_1}} = {\large\frac{p_2V_2}{T_2}}\) などと表現することもあります。このとき、\(T\) の単位は絶対温度 [K] です。\(p\) と \(V\) については、両辺が揃っていれば単位は何でもかまいません。
ボイル⋅シャルルの法則
\(\boldsymbol{{\large\frac{p_1V_1}{T_1}} = {\large\frac{p_2V_2}{T_2}}}\)