回折格子

回折格子による光の干渉

ガラス板の表面に1cm当たり数百本～数千本もの割合で直線の溝を等間隔に刻んだものを回折格子（かいせつこうし＊ 読み方注意！かいせきでもなければ、かくしでもない 閉じる ）といいます。溝の部分では光は散乱して通りにくく、溝以外の平らな部分を光が通ります＊ イラストでは
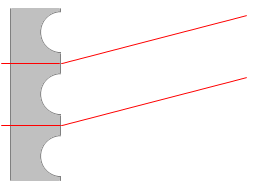このように表現したり、

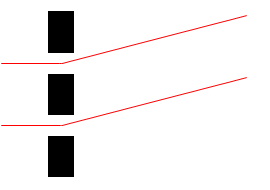このように表現したりします。 閉じる 。つまり回折格子は、ヤングの干渉実験における2つのスリットを多数のスリットに置き換え、間隔 \(d\) をとても小さくしたものといえます。そして回折格子におけるこの間隔 \(d\) を格子定数といいます。

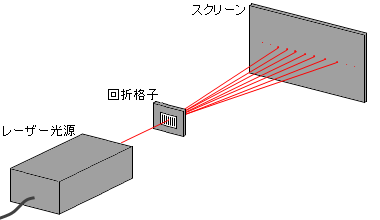回折格子の手前からレーザー光線（単一波長の光）を当てると回折格子の後方のスクリーンに干渉縞が現れます。原理はヤングの干渉実験とまったく同じです。ヤングの干渉実験では波源であるスリットが2つだったのに対し、回折格子の実験では波源であるスリットが多数あるので、干渉縞はよりくっきりと映ります。また、ヤングの干渉実験に比べ、スリットの間隔 \(d\) がとても小さいので干渉縞の縞の間隔が大きくなります。

明線・暗線の条件

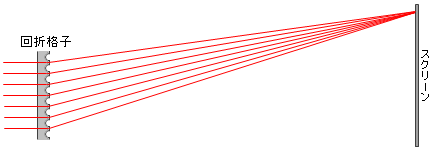回折格子の実験における \(d\) と \(λ\) の関係を求めてみます。

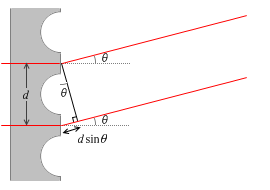ヤングの干渉実験とまったく同じように考えますと、隣り合うスリット間の光路差は \(d\sinθ\) で、この光路差が波長のちょうど整数倍になるところに明線ができ、波長の整数倍に半波長足したようになるところに暗線ができます。

ヤングの干渉実験においては、\(\sinθ ≒ \tanθ\) という近似を行ったのですが、それは \(θ\) があまりにも小さかったからです。回折格子の干渉実験においてはその必要はありません。

\(m\)次の干渉縞

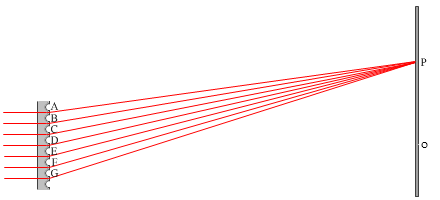左図は \(m = 1\) の明線ができている場面です。1次の干渉縞といいます。
たとえば、
AP=100\(λ\)、BP=101\(λ\) で |AP-BP|=1\(λ\)
BP=101\(λ\)、CP=102\(λ\) で |BP-CP|=1\(λ\)
CP=102\(λ\)、DP=103\(λ\) で |CP-DP|=1\(λ\)
DP=103\(λ\)、EP=104\(λ\) で |DP-EP|=1\(λ\)
… ということです。

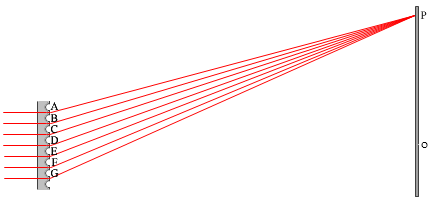左図は \(m = 2\) の明線ができている場面です。2次の干渉縞といいます。
たとえば、
AP=110\(λ\)、BP=112\(λ\) で |AP-BP|=2\(λ\)
BP=112\(λ\)、CP=114\(λ\) で |BP-CP|=2\(λ\)
CP=114\(λ\)、DP=116\(λ\) で |CP-DP|=2\(λ\)
DP=116\(λ\)、EP=118\(λ\) で |DP-EP|=2\(λ\)
… ということです。

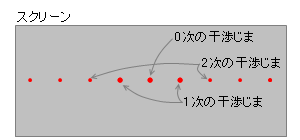
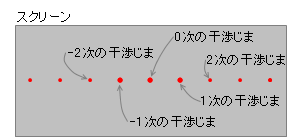上の式では \(m = 0,1,2,…\) として定義しましたが、教科書によっては \(m = 0,±1,±2,…\) と定義しているものもあります。

その場合、左図のようになります。

ここまではレーザー光（単色光）を当てた場合の話でしたが、様々な波長の光を含んだ太陽光や白熱電球の光（白色光）を当てた場合は、干渉縞の様子が少し異なります。

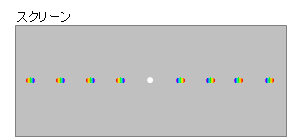明線の条件の式 \(d\)\(\sinθ\) = \(m\)\(λ\) において、同じ \(m\) でも波長 \(λ\) が異なると角度 \(θ\) が変わるからです。\(λ\) が大きくなると \(\sinθ\) が大きくなります。波長の長い赤は、わずかに外側に角度がつきます。（\(λ\) が大きくなったので \(θ\) も大きくなったのです）。波長の短い紫は、わずかに内側に寄ります。（\(λ\) が小さくなったので \(θ\) も小さくなったのです）。