様々な形態の波の干渉
波の干渉現象には、
 水面波の干渉や、
水面波の干渉や、
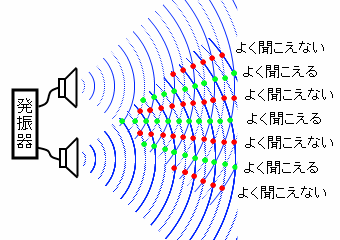 音波の干渉など、
音波の干渉など、
様々な形態がありますが、
 本項では、2箇所から出た光波(特に可視光線)の干渉について説明します。
本項では、2箇所から出た光波(特に可視光線)の干渉について説明します。
 光波と光波がぶつかって、強め合ったか弱めあったかは、スクリーンで確認します。強め合った箇所は明るくなり、弱め合った箇所は暗くなります。スクリーン上にはそれらが交互に現れ、縞模様ができます。干渉縞(かんしょうじま)といいます。
光波と光波がぶつかって、強め合ったか弱めあったかは、スクリーンで確認します。強め合った箇所は明るくなり、弱め合った箇所は暗くなります。スクリーン上にはそれらが交互に現れ、縞模様ができます。干渉縞(かんしょうじま)といいます。
波の干渉現象には、
 水面波の干渉や、
水面波の干渉や、
 音波の干渉など、
音波の干渉など、
様々な形態がありますが、
 本項では、2箇所から出た光波(特に可視光線)の干渉について説明します。
本項では、2箇所から出た光波(特に可視光線)の干渉について説明します。
 光波と光波がぶつかって、強め合ったか弱めあったかは、スクリーンで確認します。強め合った箇所は明るくなり、弱め合った箇所は暗くなります。スクリーン上にはそれらが交互に現れ、縞模様ができます。干渉縞(かんしょうじま)といいます。
光波と光波がぶつかって、強め合ったか弱めあったかは、スクリーンで確認します。強め合った箇所は明るくなり、弱め合った箇所は暗くなります。スクリーン上にはそれらが交互に現れ、縞模様ができます。干渉縞(かんしょうじま)といいます。
水面波や音波の干渉においては、2つの発振源から、同じ波長、同じ振幅、同じ位相の波を発することが容易でしたが、光波においてはこれが容易ではありません。
 光(可視光線)の波長はとても小さいものですが、それに比べて発振源として用いるライトは大き過ぎます。どの地点からどんな光が出ているのか特定できません。
光(可視光線)の波長はとても小さいものですが、それに比べて発振源として用いるライトは大き過ぎます。どの地点からどんな光が出ているのか特定できません。
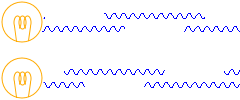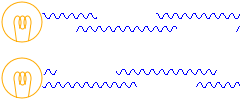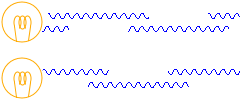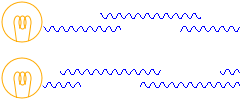 また、ライトというものは、ひと続きに連なった波を出すことができません。どうしても波が途中でぶつ切りになってしまいます。ですので、2つのライトから出る波の位相がどれだけズレているか、特定できません。
また、ライトというものは、ひと続きに連なった波を出すことができません。どうしても波が途中でぶつ切りになってしまいます。ですので、2つのライトから出る波の位相がどれだけズレているか、特定できません。
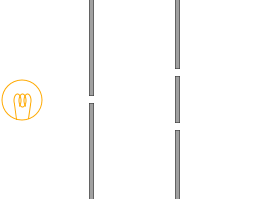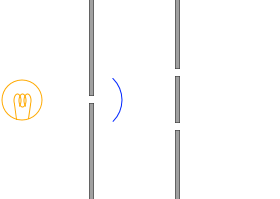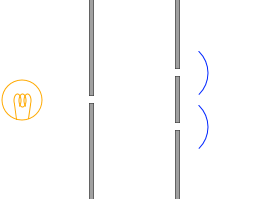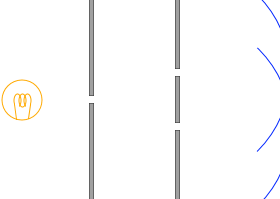 これらの問題を解決するために、ヤング
19世紀のイギリスの物理学者、トーマス・ヤング
は左図のような工夫を施しました。
これらの問題を解決するために、ヤング
19世紀のイギリスの物理学者、トーマス・ヤング
は左図のような工夫を施しました。
第一段階目の単スリット スリットというのは、ごくごく小さい隙間のことです。実験では、墨を塗ったスライドガラスにカミソリで傷をつけるなどして隙間を作ります。 で波を1つ 1つの素元波というイメージです。もちろん、厳密に「1つ」「2つ」と数えられるものではありません。 に絞り、その単スリットから等距離の位置にある2つのスリットに波を通します。すると実質的に、この第二段階目の複スリットからは位相の揃った2つの波が発射されることになります。 なぜこのように2つの段階を踏まなければならないかについて、これ以上詳しく説明することは私にはできません。もっと深く知りたい方は「干渉性 可干渉性」などのキーワードで検索してみてください。
 このように工夫されたスリットを用いて光の干渉現象を観察する実験のことをヤングの干渉実験といいます。この実験により、光が干渉することが示され、干渉することにより、光が波であることが証明されました。
このように工夫されたスリットを用いて光の干渉現象を観察する実験のことをヤングの干渉実験といいます。この実験により、光が干渉することが示され、干渉することにより、光が波であることが証明されました。
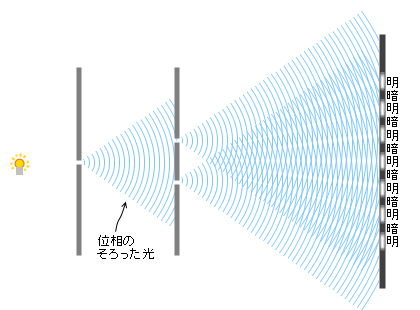 (一応ことわっておきますが、左図はかなり大げさにわかりやすく描いた図です。実際には光はこれほど大きく広がりませんし、スリットの隙間の幅も 1mm 以下ですし、複スリットからスクリーンまでの距離も 1m 以上あります。 )
(一応ことわっておきますが、左図はかなり大げさにわかりやすく描いた図です。実際には光はこれほど大きく広がりませんし、スリットの隙間の幅も 1mm 以下ですし、複スリットからスクリーンまでの距離も 1m 以上あります。 )
(また、左図では光源として白熱電球のようなイラストを描いてしまいましたが、実際に実験をするときは、単色光(レーザー光)を用いる方が良いです。白熱電球では様々な波長の波が発せられてしまうので、縞模様がぼやけてしまいます。)
(レーザー光を光源として用いるなら、第一段階目の単スリットは必要ありません。しかし、2つのレーザー光を2つの光源として、複スリットの代わりにすることはできません。位相が合わせられません。)
干渉する2つの光波がたどる光学的距離の差を光路差といいますが、
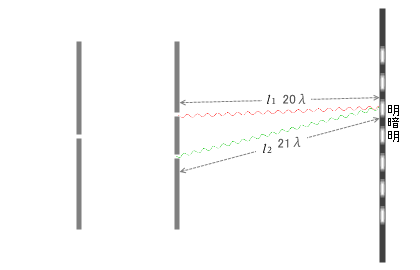 2つの光波のスクリーンまでの光路差が光波の波長のちょうど整数倍になるような地点で波は強め合い明線ができます。光路差が整数倍に半波長足したようになる地点では暗線ができます。(『干渉の条件』参照)
2つの光波のスクリーンまでの光路差が光波の波長のちょうど整数倍になるような地点で波は強め合い明線ができます。光路差が整数倍に半波長足したようになる地点では暗線ができます。(『干渉の条件』参照)
明線ができる条件 \(| l_1 - l_2 | = mλ\)
暗線ができる条件 \(| l_1 - l_2 | = (m + {\large\frac{1}{2}})λ\)
\((m = 0,1,2,…)\) ……①
たとえば上図は、赤波 \(l_1 = 20λ\) 、緑波 \(l_2 = 21λ\) で、\(| 20λ - 21λ | = 1λ\) となり、明線ができている場面です。
ここで、\(| l_1 - l_2 |\) について、別の量を用いて表現できないか考えてみます。
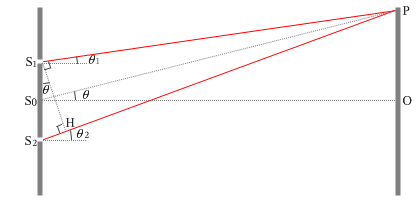 左図のように符号を割り振りますと、
左図のように符号を割り振りますと、
3つの線分S1P、S0P、S2Pは平行とみなせます。実際にはS1S2は 1mm 以下でS0Oは 1m 以上あるからです。ですので、∠S2S1H と \(θ_1\) と ∠PS0O と \(θ_2\) は全て等しくなります。
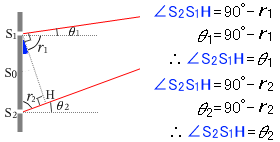 ∠S2S1H と \(θ_1\) が等しくなる(∠S2S1H と \(θ_2\) も等しくなる)のはわかりますでしょうか。
∠S2S1H と \(θ_1\) が等しくなる(∠S2S1H と \(θ_2\) も等しくなる)のはわかりますでしょうか。
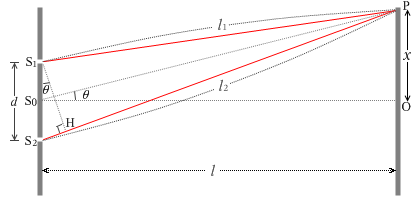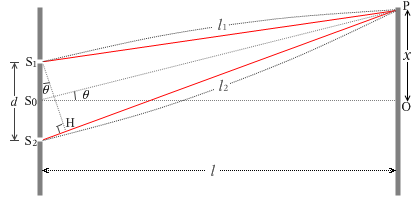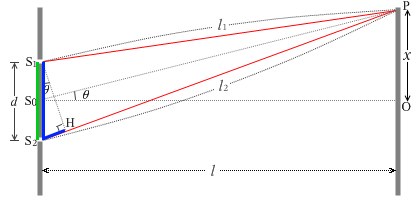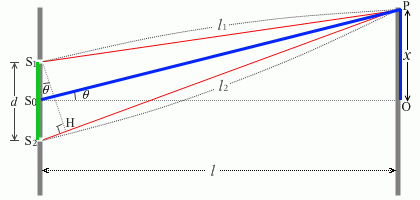 さらに左図のように符号を割り振りますと、
さらに左図のように符号を割り振りますと、
(三角比の sin については sin・cos 参照)
\(| l_1 - l_2 |\) ≒ S2H = S1S2\(\sinθ\) = \(d\)\(\sinθ\) = \(d\)\(\color{blue}{{\large\frac{x}{\rm{S_0 P}}}}\)
また、\(θ\) は極めて小さいから、
\({\color{blue}{\large\frac{x}{\rm{S_0 P}}}} = \sinθ ≒ \tanθ = {\large\frac{x}{l}}\)
よって、
\(| l_1 - l_2 | ≒ {\large\frac{dx}{l}}\) ……②
となります。
\(\sinθ ≒ \tanθ\) について説明します。
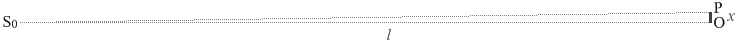
ヤングの干渉実験において実際には△S0POは上図のように非常にうす平たい三角形になってます。ここまで \(θ\) が小さい場合、S0P ≒ \(l\) であるから、
\(\sinθ = {\large\frac{x}{\rm{S_0 P}}} ≒ {\large\frac{x}{l}} = \tanθ\)
となります。
( 回折格子の場合はこの近似は必要ありません。\(θ\) がある程度の大きさがあるので、角度が測定可能です。\(θ\) が測定できないほど小さいときに、この近似が必要になってきます。)
というわけで、②式を①式に代入してまとめますと以下のようになります。
ヤングの干渉実験
明線の条件 \(\boldsymbol{{\large\frac{dx}{l}} = mλ}\)
暗線の条件 \(\boldsymbol{{\large\frac{dx}{l}} = (m+{\large\frac{1}{2}})λ}\)
\((m = 0,1,2,…)\)
上の条件式から干渉縞の間隔の大きさを求めてみます。
明線の条件式 \({\large\frac{dx}{l}} = mλ\) を変形しますと、
\(x = {\large\frac{mlλ}{d}}\)
このときの \(m\) という数は、その縞が中央から何番目であるかを表しています。
 2つの光波の光路差が 0 のときは 0番目、つまり中央という意味です。
2つの光波の光路差が 0 のときは 0番目、つまり中央という意味です。
上の方で、赤波 \(l_1=20λ\) 、緑波 \(l_2 = 21λ\) で、\(| 20λ - 21λ | = 1λ\) という例を示しましたが、これは \(m = 1\) のときということです。
光路差が大きくなると \(m\)(\(x\) も)が大きくなります。
というわけで、縞の間隔 \(Δx\) は \(x_{m+1} - x_m\) です。
\(Δx = x_{m+1} - x_m\)
\(= {\large\frac{(m+1)lλ}{d}} - {\large\frac{mlλ}{d}}\)
\(= {\large\frac{lλ}{d}}\)
この式を用いますと、縞の間隔 \(Δx\) とスクリーンまでの距離 \(l\) とスリット間の距離 \(d\) から、光波の波長 \(λ\) が求められます。あるいは、縞の間隔 \(Δx\) を大きくするには、\(l\) または \(λ\) を大きくするか、\(d\) を小さくすればいい、とわかります。
ちなみに、\(d\)(2つのスリットの間隔)を小さくするということは下のイラストのようなことです。
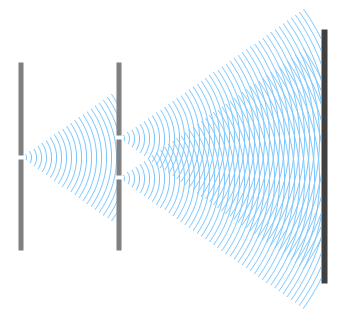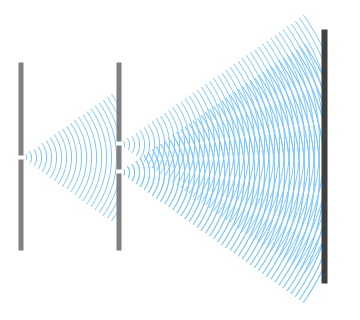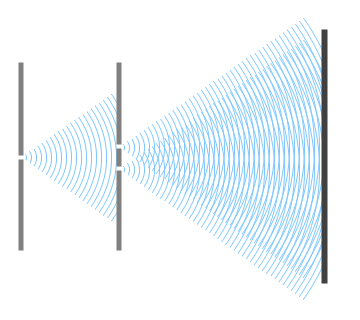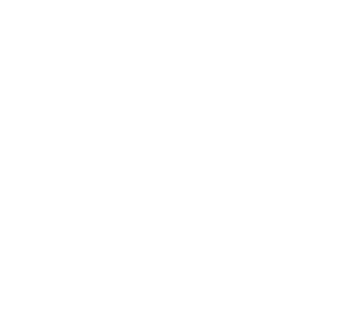 縞の間隔が広がるのがわかると思います。モアレと同じ原理です。
縞の間隔が広がるのがわかると思います。モアレと同じ原理です。
②式 \(| l_1 - l_2 | ≒ {\large\frac{dx}{l}}\) を求める別の方法を紹介しておきます。

この式において、\(x\) や \(d\) が \(l\) にくらべて十分小さいとすると、\(a\) が十分小さいときの近似式 \((1 + a)^n ≒ 1 + na\) が適用できます。この近似式の導出方法はここでは説明しませんが、興味のある方は「テイラー展開 近似式」などのキーワードで検索してみてください。
近似しますと、
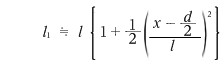
まったく同様にして \(l_2\) を求めますと、
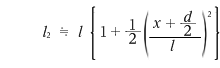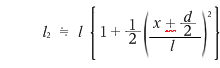
よって光路差は、
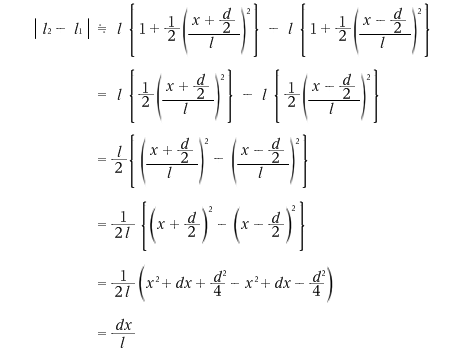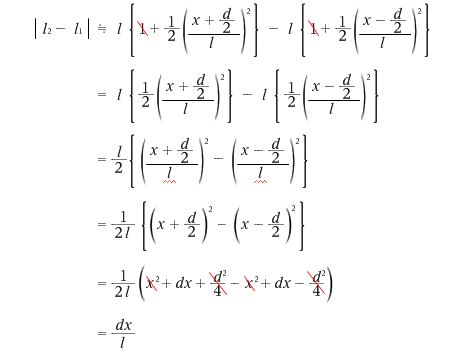
と求められます。