凸面鏡のつくる像
各量の関係を求める
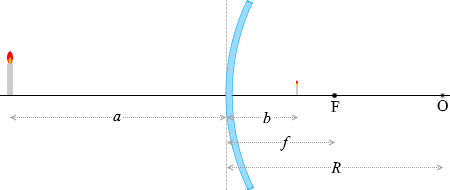
物体から出る光線が凸面鏡で反射して像を作るとき、以下の各量の関係を考えてみます。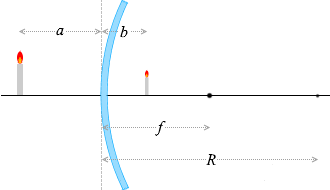
物体と鏡との距離：\(a\)
鏡と像との距離：\(b\)
焦点距離：\(f\)
球の半径：\(R\)
代表的な光線
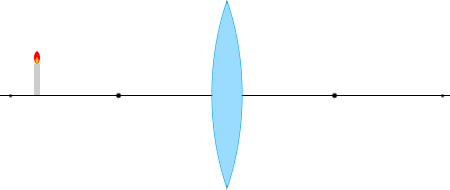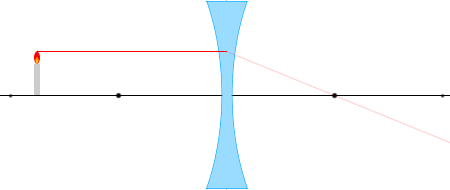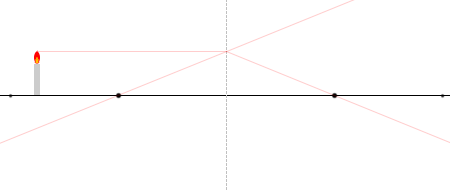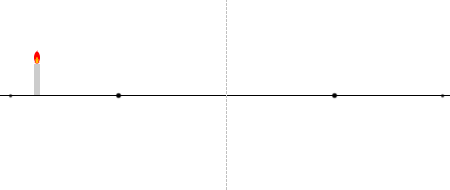
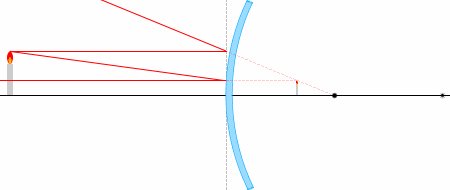
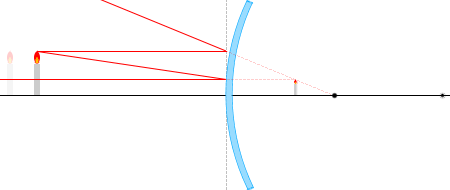
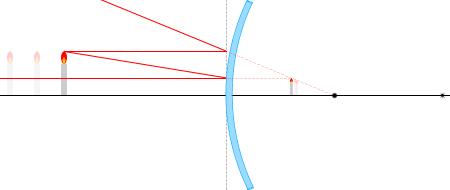
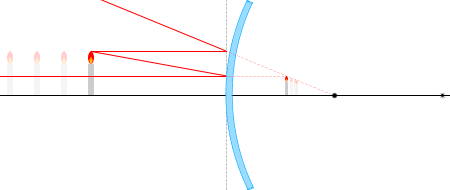
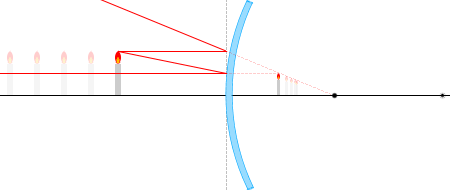
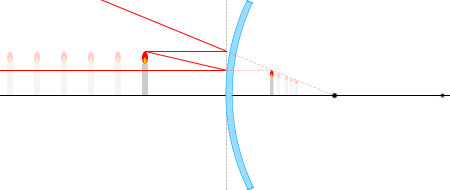
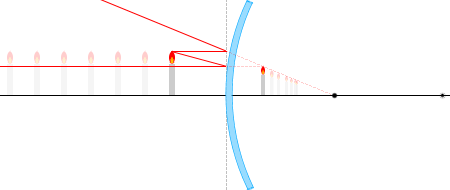
物体から出る光線の経路は何通りも考えられますが、代表的なものは以下の4本です。
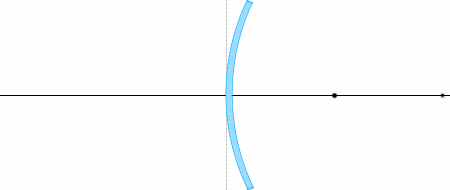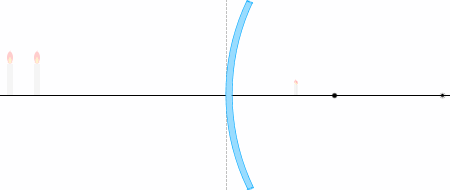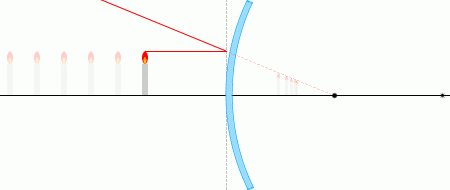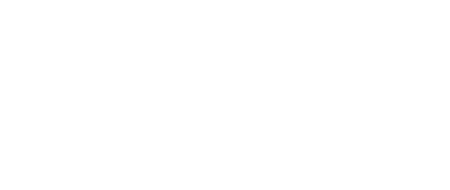
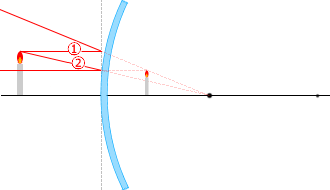① 光軸に平行な光線は反射して焦点から出たように進む。
② 焦点に向かう光線は反射して光軸に平行に進む。
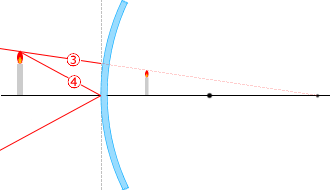
③ 球の中心に向かう光線は反射して再び同じ経路を戻る。
④ 反射の法則により入射角=反射角。
これらのうちのどれか2本を使って考えていきます。解法は何通りもあります。
凸面鏡のつくる像
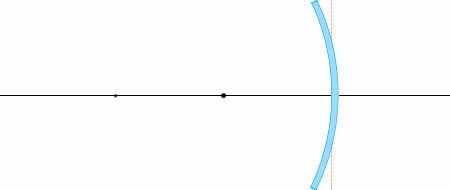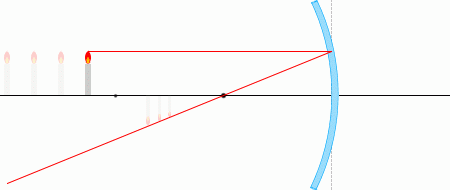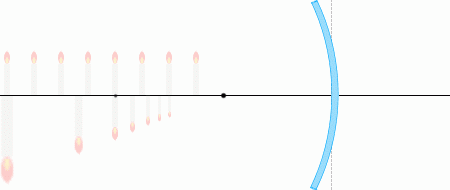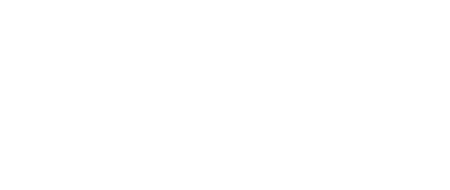
上で示した光線のうち、たとえば①と②の光線によってできる三角形を用いて考えてみます。
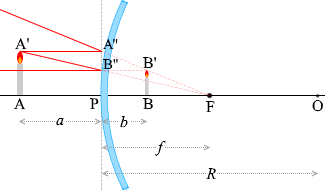左図のように符号を振ります。
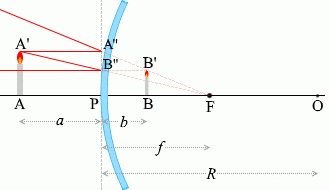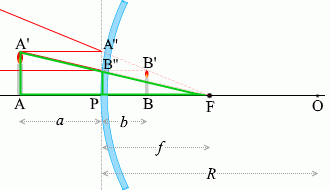△AA'Fと△PB''Fは相似である（とみなせる）から、
\({\large\frac{{\rm PB''}}{{\rm AA'}}} = {\large\frac{{\rm PF}}{{\rm AF}}} = {\large\frac{f}{a+f}}\)
であり、また、PB'' = BB' であるから上式に代入して、
\({\large\frac{{\rm BB'}}{{\rm AA'}}} = {\large\frac{f}{a+f}}\) ……①
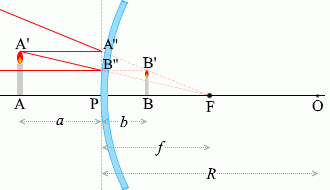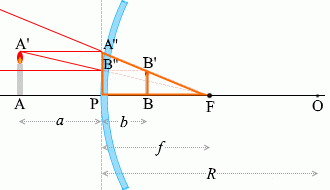△PA''Fと△BB'Fは相似だから、
\({\large\frac{{\rm BB'}}{{\rm PA''}}} = {\large\frac{{\rm BF}}{{\rm PF}}} = {\large\frac{f-b}{f}}\)
であり、また、PA'' = AA' であるから上式に代入して、
\({\large\frac{{\rm BB'}}{{\rm AA'}}} = {\large\frac{f-b}{f}}\) ……②
①式と②式は左辺が共通だから、
\({\large\frac{f}{a+f}} = {\large\frac{f-b}{f}}\)
∴ \(f^2 = (f - b)(a + f)\)
∴ \(f^2 = af - ab + f^2 - bf\)
∴ \(0 = af - ab + 0 - bf\)
∴ \(bf - af = - ab\) 両辺を \(abf\) で割って
∴ \({\large\frac{bf}{abf}} - {\large\frac{af}{abf}} = - {\large\frac{ab}{abf}}\)
∴ \({\large\frac{1}{a}} - {\large\frac{1}{b}} = - {\large\frac{1}{f}}\) ……③
これが凸面鏡の写像公式です。
この式をよく見ますと、\(a → ∞\) のとき（左辺第一項が 0 になって） \(b = f\) となることが分かります。さらに、下で説明するように倍率は \({\large\frac{b}{a}}\) でありますから、\(a → ∞\) の場合はほぼ 0 です。物体を凸面鏡から遠く離して置くと、焦点付近に極小の像ができるということです。
倍率
倍率というのは物体がどのくらい拡大、縮小されたかという割合で、つまり \({\large\frac{{\rm BB'}}{{\rm AA'}}}\) のことです。\(m\) とおきます。
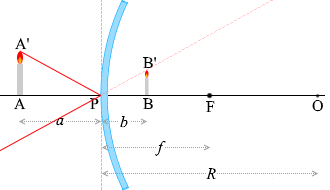上で示した代表的な光線のうち、④の線によって作られる左図のような相似の三角形、△AA'Pと△BB'P
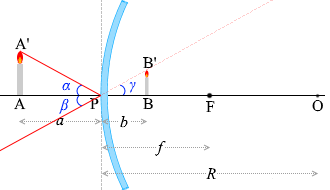
反射の法則により \(α = β\)
対頂角は等しいので \(β = γ\)
よって \(α = γ\)
よって △AA'P と △BB'P は相似。
を考えれば \(m = {\large\frac{{\rm BB'}}{{\rm AA'}}} = {\large\frac{b}{a}}\) であることは一目瞭然です。
像の倍率というのは、鏡からの距離の比率と同一です。
また、凸面鏡の場合は倍率が 1.0 を超えることがありません。
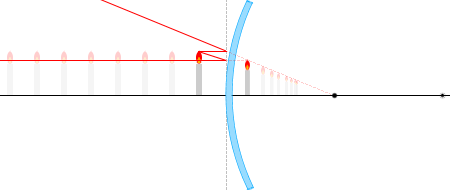BB'がAA'より大きくならないのです。
像が常に縮小されるのです。凸面鏡は拡大鏡としては使えません。凹レンズもそうでした。
正立虚像
凸面鏡によって作られる像は、鏡の手前（左図における左側）から見たときに、鏡の向こう（＝鏡の後方＝鏡の裏側）に像があるように人間が脳内で感じるものです。つまり虚像です。そして倒立像ではなく正立像です。
凹面鏡の場合は、物体を焦点より遠くに置いたときと近くに置いたときで像の出来方に違いがありましたが、凸面鏡のときは違いはありません。遠くにおいても近くにおいても正立虚像です。
焦点距離は半径の半分
次に、焦点距離と半径の関係を探ってみます。
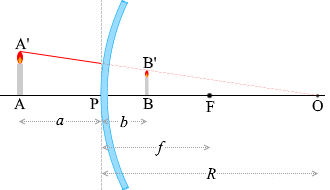上で示した代表的な光線の③の線によって作られる三角形について考えてみます。
すると、△AA'Oと△BB'Oは相似だから、
\({\large\frac{{\rm BB'}}{{\rm AA'}}} = {\large\frac{{\rm BO}}{{\rm AO}}} = {\large\frac{R-b}{a+R}}\)
上で説明した倍率の式
\(m = {\large\frac{{\rm BB'}}{{\rm AA'}}} = {\large\frac{b}{a}}\)
と合わせますと、
\({\large\frac{R-b}{a+R}} = {\large\frac{b}{a}}\)
∴ \(aR - ab = ab + bR\)
∴ \(aR - bR = 2ab\) 両辺を \(abR\) で割って
∴ \({\large\frac{aR}{abR}} - {\large\frac{bR}{abR}} = {\large\frac{2ab}{abR}}\)
∴ \({\large\frac{1}{b}} - {\large\frac{1}{a}} = {\large\frac{2}{R}}\)
∴ \({\large\frac{1}{a}} - {\large\frac{1}{b}} = - {\large\frac{2}{R}}\)
この式と上で示した凸面鏡の写像公式③式
\({\large\frac{1}{a}} - {\large\frac{1}{b}} = - {\large\frac{1}{f}}\)
を見比べますと、
\(- {\large\frac{1}{f}} = - {\large\frac{2}{R}}\)
∴ \(f = {\large\frac{R}{2}}\)
となっていて、焦点距離は半径の半分、と分かります。凹面鏡の場合と同じです。
凸面鏡のまとめ
\(b\) も \(f\) も正の値のみをとるとすると凸面鏡の写像公式は以下のように表現できます。
\({\large\frac{1}{a}} - {\large\frac{1}{b}} = - {\large\frac{1}{f}}\)
像は常に正立虚像
\(m = {\large\frac{b}{a}} < 1\)
←前項の凹面鏡
本項の凸面鏡→
