全反射

全反射

光が、ある媒質からある媒質へ屈折して進むとき、実際には一部は反射して戻ってきます。そしてある条件のもとでは全てが反射して戻ってきます。

光が屈折率の大きい媒質から小さい媒質へ進むとき、入射角を徐々に大きくしていくと、あるところで屈折角が 90° になり、さらに入射角を大きくすると光は向こう側へは行かず全部反射するようになります。全反射といいます。ホイヘンスの原理によって説明できます。

臨界角

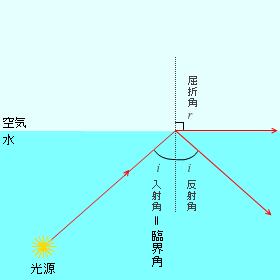全反射が起こるかどうかぎりぎりのときの入射角を臨界角といいます。このとき屈折角は 90° です。

臨界角を \(i_0\) として、前項の　\(n_{12} = {\large\frac{\sin i}{\sin r}} = {\large\frac{n_2}{n_1}}\)　式に代入しますと、\(\sin90°\! =\! 1\) ですから、

　　　\(n_{12} = {\large\frac{\sin i_0}{\sin90°}} = {\large\frac{\sin i_0}{1}} = {\large\frac{n_2}{n_1}}\)

つまり、以下のようになります。

\(\sin\) の最大値は 1 であるので、\(n_1\) より \(n_2\) の方が大きくなることはありません。つまり、屈折率の小さい媒質から大きい媒質へ進むときは臨界角は存在しません。全反射が起こらないということです。＊
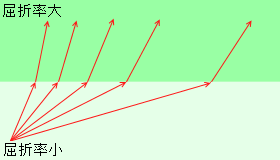
屈折率が小さい媒質から屈折率が大きい媒質へ進む場合は、屈折角がどうしても 90° になりません。
補足ページもご参照ください。 閉じる

さらに、\(n_1\) と \(n_2\) の差が大きいときの方が \(i_0\) が小さい、これはつまり屈折率の差が大きいときの方が全反射が起こりやすい、ということがいえます。

空気へ向かう場合

光が、ある媒質（屈折率を\(n\)とします）から空気（屈折率が1）へ向かう場合は、上式は以下のように表せます。

　　　\(\sin i_0 = {\large\frac{1}{n}}\)

水から空気へ向かうときの値

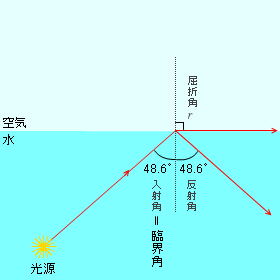たとえば、光が水から空気へ向かう場合の臨界角は、上式に \(n =\) 1.333 を代入して、

　　\(\sin i_0 = {\large\frac{1}{n}} = {\large\frac{1}{1.333}} ≒ 0.750\)

この数値を三角関数表あるいは高機能電卓を使って調べると、\(i_0 ≒ 48.6°\) とわかります。

全てを覆う必要は無い

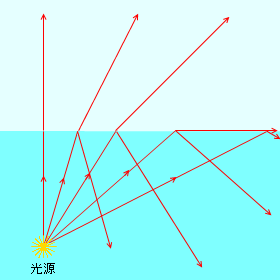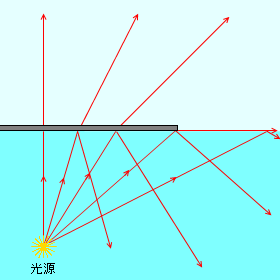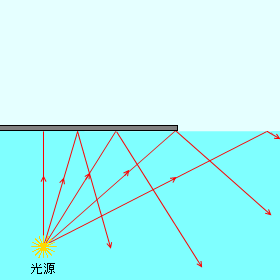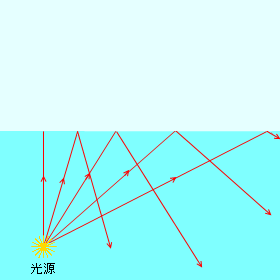入射角が臨界角より小さくなるような領域を障害物で覆うと、光は向こう側に到達できなくなります。上から見たときに光源が見えなくなるということです。このとき、入射角が臨界角より大きくなるような領域は覆う必要はありません。

光ファイバー

インターネット通信などに使われる光ファイバーケーブルは、屈折率の大きいガラスなどの素材を中心部に使い、外周部に屈折率の小さい素材を使い、光信号が中心部を全反射しながら進んでいくという仕組みの通信ケーブルです。銅線ケーブルに比べて、信号の漏れが少ない、外部からの電磁波の影響を受けにくいなどの特徴があり、長距離で大容量の通信に適しています。