弦の振動は両端が節
ピンと張った弦を弾くと、横波が発生し、両端で反射し、重なり合い、定常波ができます。弦が空気を振動させて音を出したとき、一定の高さの音が出ます。
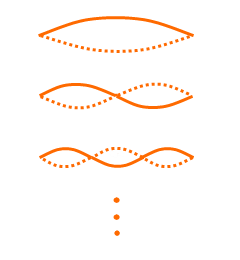 弦というものは両端が固定されているので、定常波の形は左図のようなパターンになります。両端が節となるような波長の波は残り、そうでない波長の波は消えていきます
波は両端の固定端とケンカして減衰していきますが、両端がちょうど節となるような波はあまり固定端とケンカせず、そうでない波は固定端とケンカしてしまい、減衰しやすいです。
。
弦というものは両端が固定されているので、定常波の形は左図のようなパターンになります。両端が節となるような波長の波は残り、そうでない波長の波は消えていきます
波は両端の固定端とケンカして減衰していきますが、両端がちょうど節となるような波はあまり固定端とケンカせず、そうでない波は固定端とケンカしてしまい、減衰しやすいです。
。
これらの波のうち、腹が1つの振動を基本振動、腹が2つの振動を2倍振動、腹が3つの振動を3倍振動、…といいます。弦の固有振動数は複数あり、それらの振動は同時に起こっています
複数の振動が同時に起こっているので波形は複雑になりますが、一番波形がハッキリしているのは基本振動です。それ以外は振幅がとても小さい波形です。
弦の長さの¼に当たる部分を強く弾けば、2倍振動の波形が比較的大きく現れるはずです。
弦を強くピンと張れば、ほぼ基本振動の波形しか見えなくなるはずです。
。
(注意して欲しいのが、1波長というのは ではなく
ではなく であることです。
であることです。 は½波長です。弦の振動の形は½波長の自然数倍です。 )
は½波長です。弦の振動の形は½波長の自然数倍です。 )
弦の長さと波長の関係
弦の長さと波長の関係を求めてみます。弦の長さを \(l\) [m] 、\(n\)倍振動 \((n=1,2,3,…)\) での波長を \(λ_n\) [m] とします。
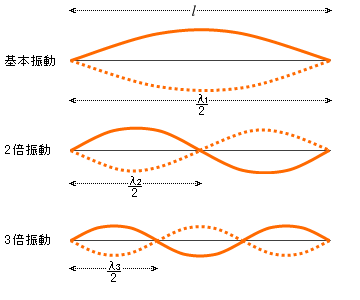
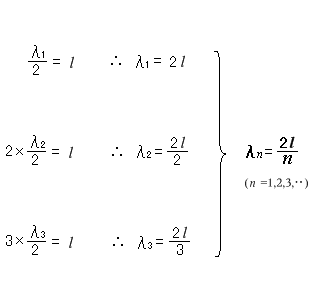
賢い方は暗算で求められるかもしれません。
\(λ_1 = 2l\) というのは、
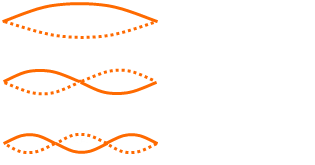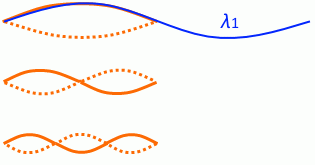 ということですし、
ということですし、
\(λ_2 = {\large\frac{2l}{2}}\) というのは、
 ということですし、
ということですし、
\(λ_3 = {\large\frac{2l}{3}}\) というのは、
 ということです。
ということです。
弦の固有振動数
弦を伝わる波の速さを \(v\) [m/s] とすると、\(v = fλ\) ですので、この式に上式を代入して振動数 \(f_n\) [Hz] を求めると、
\(f_n = {\Large\frac{v}{λ_n}} = {\Large\frac{v}{\frac{2l}{n}}} = {\large\frac{v}{2l}}n\)
この式をよく見ますと、\(v\) と \(l\) は定数なので、\(n\) が2倍になると \(f_n\) も2倍になる、すなわちこれは、\(n\)倍振動の振動数は基本振動の振動数の \(n\)倍である、ということがわかります。(弦を弾いて 440Hz の音を出したとき、880Hz、1320Hz、1760Hz、…の音も小さいですが同時に出ています。)
また、弦を伝わる波の速さというのは、弦の張力を \(S\) [N]、1m 当たりの質量(線密度)を \(ρ\) [kg/m] とすると、
\(v = {\large\sqrt{\frac{S}{\rho}}}\)
という式で与えられます
\(ρ\) は ロー と読みます。ギリシャ文字です。小文字です。張力の \(S\) は大文字を用いることが多いです。
\(v = {\large\sqrt{\frac{S}{\rho}}}\) の式の導出はここでは説明しません。難解というわけではありませんがかなり面倒です。おおまかにいうと、張力が大きいと弦の復元力も大きくなり弦の振れ戻りが速くなり波が速く伝わり、また、弦が重い(密度が大きい)と慣性が大きくなり弦の振れ戻りが遅くなり波が遅くなる、という感じです。詳しいことは「弦 波 速さ」などのキーワードで検索してみてください。
。この式を上式に代入します。
\(f_n = {\large\frac{v}{2l}}n = {\large\frac{n}{2l}\sqrt{\frac{S}{\rho}}}\)
この式から、\(f_n\) を大きくする(=音を高くする)には、
- 弦の長さ \(l\) を小さくする。(ギターでは、根元に近いフレットを押さえた方が音が高くなる。)
- 張力 \(S\) を大きくする。(ギターでは、調律するときペグを巻き上げた方が音が高くなる。)
- 線密度 \(ρ\) を小さくする。(ギターでは、弦が軽い方が音が高い。)
ということがわかります。

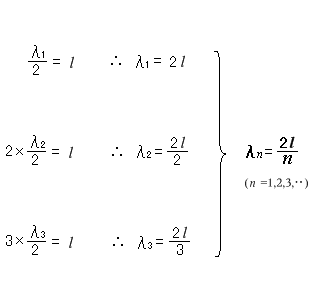
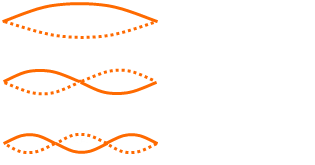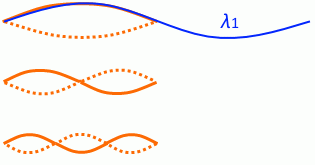 ということですし、
ということですし、 ということですし、
ということですし、 ということです。
ということです。