単振り子

微小振動の単振り子

糸の一端を固定し、他端におもりを付けて吊るし、鉛直面内で振らせるもの＊おもりを水平面内で振らせれば円錐振り子です。
　閉じるを単振り子といいます。

この単振り子の振幅が小さい（振れ角が小さい）とき＊振れ角が小さいときというのは、おもりの軌道が円弧というより直線に近くなっているときです。
　閉じる、そのおもりの運動は単振動とみなせます。
『単振り子の力学的エネルギー』項では力学的エネルギー保存の法則から各地点でのおもりの速さを求めました。
本項では、微小振動する単振り子が単振動することに着目して、往復運動するおもりの周期を求めます。

微小振動の単振り子の復元力

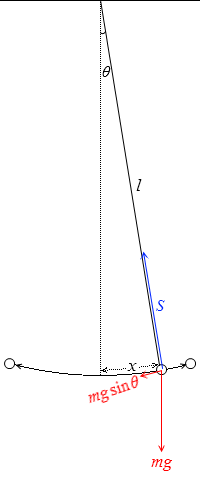糸の長さを l [m] 、おもりの質量を m [kg] 、糸と鉛直線とのなす角を θ [rad] 、最下点の位置を O 、O点から円弧に沿った変位を x [m] （左図において右向きを正とする）、重力加速度を g [m/s²] とします。

おもりにはたらく力は、張力 S [N] と重力 mg [N] ですが、このうち円弧方向に関わる力は mgsinθ です。張力 S や mgcosθ はおもりの円弧方向の運動には関わりません。

また、張力 S と重力 mg の合力が mgsinθ というわけではないので勘違いしないでください。＊ 単振り子と円錐振り子を混同しないでください。運動の方向が違います。
しかも、円錐振り子における合力は mgsinθ ではなく mgtanθ です。

さらにいいますと、単振り子における糸方向（張力の方向）の力のつり合いの関係は
　　張力S = mgcosθ + 反心力
となっています。
反心力とは遠心力のことです。
最上点（左端、右端のこと）では反心力は 0 です。
最下点を通過するときは反心力は最大となります。
　閉じる

x が正のとき（左図においておもりが鉛直線より右側にあるとき）に mgsinθ のはたらく向きは左向きで、x が負のときは mgsinθ のはたらく向きは右向きなので、おもりの円弧方向にはたらく力 F [N] は - を付けて以下のように表せます。

　　F = - mgsinθ

この式を変形していきます。

x = θl ＊ 半径 r の円において中心角 1rad の円弧の長さが r なのだから、
半径 l の円において中心角 0.8rad の円弧の長さは 0.8l
半径 l の円において中心角 1.2rad の円弧の長さは 1.2l
半径 l の円において中心角 θrad の円弧の長さは θl
　閉じるであるから θ = \(\large{\frac{x}{l}}\) 。よって上式は、

　　F = - mgsin\(\large{\frac{x}{l}}\)

そしていま、θ は十分小さいものとしているので近似式　sinθ ≒ θ ＊ ラジアン三角関数表によると、
　θ = 0.01　のとき　sinθ = 0.0100
　θ = 0.10　のとき　sinθ = 0.0998
　θ = 0.20　のとき　sinθ = 0.1987
　θ = 0.30　のとき　sinθ = 0.2956
となっています。
詳しくは数学の教科書を見てください。
下の『振幅が大きい場合』もご参照ください。
　閉じるが成り立ちます。よって上式は近似的に以下のように表せます。

　　　　F = - mgsin\(\large{\frac{x}{l}}\) = - mg\(\large{\frac{x}{l}}\) = - \(\large{\frac{mg}{l}}\)x

\(\large{\frac{mg}{l}}\) の部分は定数だから、上式は、力の方向は変位と逆向きでその大きさは変位の大きさに比例する、ということを表しており、これはまさに復元力であり、おもりは単振動をする、と分かります。

微小振動の単振り子の周期

おもりの円弧方向の加速度＊円弧方向でない加速度というのもあって、それは糸の方向（半径方向）の加速度、つまり向心加速度のことです。
　閉じるを a [m/s²] とすると、運動方程式は

　　　　ma = F = - \(\large{\frac{mg}{l}}\)x

よって、加速度は

　　　　a = - \(\large{\frac{g}{l}}\)x

角振動数を ω [rad/s] とすると、単振動の加速度の式は

　　　　a = - ω²x

と表され、これを上式と比較すると＊　a = - \(\large{\frac{g}{l}}\)x
における x は円弧方向の変位で、
　a = - ω²x
における x は x軸における変位で、
”円弧”と”直線”の違いがありますが、同じものと近似して考えています。
　閉じる、

　　　　\(\large{\frac{g}{l}}\) = ω²

つまり、

　　　　ω = \(\sqrt{\large{\frac{g}{l}}}\)

さらに単振動の周期を T [s] とすると　T = \(\large{\frac{2\pi}{\omega}}\)　であるから、

となります。

この式をよく見ると、微小振動の単振り子の周期は糸の長さと重力加速度のみで決まり、おもりの質量や振幅には無関係であることが分かります。このことを振り子の等時性＊ガリレオ・ガリレイが発見しました。

単振り子と円錐振り子では運動の方向が異なるのですが、『円錐振り子』項の『解釈』も一応ご参照ください。
　閉じるといいます。

ということは、たとえば周期が 1s となる振り子の長さは決まっているということになります。

T = 1 、g = 9.8 として上式に代入しますと、

　　　　1 = 2π\(\sqrt{\large{\frac{l}{9.8}}}\)　　　　両辺を2乗して

　　　　1² = 4π²\(\large{\frac{l}{9.8}}\)

　　　　l = \(\large{\frac{9.8}{4\pi^2}}\) ≒ \(\large{\frac{9.8}{4\times3.14^2}}\) ≒ 0.248

つまり、振り子の長さが約24.8cmのときにおもりは1秒で1往復するということです。このときおもりの質量は無関係ということです。なんでもいいから長さ24.8cmのひもを吊るして微小振動させれば、だいたい1往復が1秒です。1往復2秒にするには上式の l を 4倍にする必要があるので約99cmの長さが必要です。

また逆に、この原理を使うと地球上の各地点で微妙に違う重力加速度を測定することができるということにもなります。振り子の長さと往復にかかった時間を上式に代入すれば重力加速度が導き出せます。

振幅が大きい場合

単振り子の振幅が大きいときは、近似式　sinθ ≒ θ　が成り立たないので、単振動とみなせなくなるわけですが、具体的にいうと以下のようなことです。

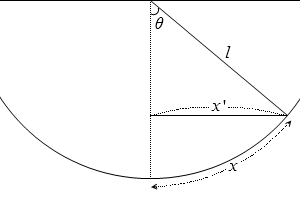sinθ というのは左図でいうと \(\large{\frac{\ x'}{l}}\) のことです。

θ というのは上でも解説しましたが \(\large{\frac{\ x}{l}}\) のことです。

振幅が大きい、つまり振れ角 θ が大きいときはこの２つが同じとはみなせません。

今の若い方は振り子時計というものを見たことがないかもしれませんが、実際の振り子時計は振幅がそれほど小さいわけではないです。それでも正確な時を刻むのは、機械的に補正を行なっているからのようです。