図1のように起電力 V 、内部抵抗 r の n個の電池E1、E2、…、En と n個のスイッチS1、S2、…、Sn、抵抗 R を接続した回路がある。
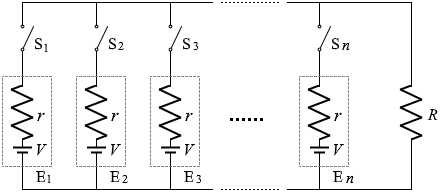 図 1
図 1
(問1)二つのスイッチS1、S2のみを閉じたとき、抵抗 R に流れる電流はいくらか。
(問2)スイッチS1、S2、…、Sn のすべてを閉じたとき、電池E1の内部抵抗に発生する単位時間あたりのジュール熱はいくらか。
(問3)すべてのスイッチS1、S2、…、Sn を閉じた状態で抵抗 R に流れる電流を I とする。n個の電池を図2のように起電力が V で内部抵抗が r' の1個の電池Eに置き換え、抵抗 R に同じ大きさ I の電流が流れるようにしたい。内部抵抗 r' をどのようにとればよいか。
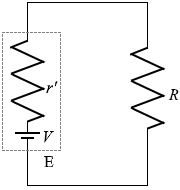 図 2
図 2
#センター05本試
(問1)
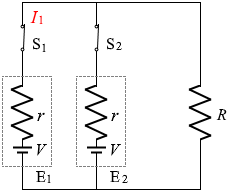 E1 に流れる電流を I1 としますと、
E1 に流れる電流を I1 としますと、
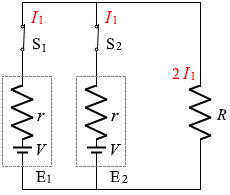 まったく同じ部品の E2 にも同じ大きさの電流が流れているはずで、さらに、キルヒホッフの第1法則により抵抗 R には 2I1 の電流が流れているはずです。
まったく同じ部品の E2 にも同じ大きさの電流が流れているはずで、さらに、キルヒホッフの第1法則により抵抗 R には 2I1 の電流が流れているはずです。
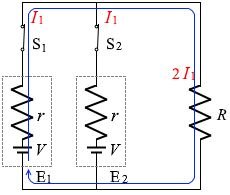 また、左図のような経路についてのキルヒホッフの第2法則の式を立てますと、
また、左図のような経路についてのキルヒホッフの第2法則の式を立てますと、
V = 2I1R + I1r
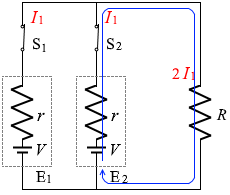
このような経路を考えてもまったく同じ式になります。
∴ I1 = \(\large{\frac{V}{2R+r}}\)
と I1 が求まり、
抵抗 R を流れる電流は
2I1 = \(\large{\frac{2V}{2R+r}}\)
と求まります。
(問2)スイッチS1、S2、…、Sn のすべてを閉じたとき、電池E1の内部抵抗に発生する単位時間あたりのジュール熱はいくらか。
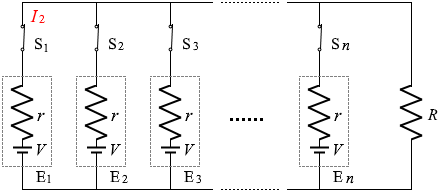 E1 に流れる電流を I2 としますと、
E1 に流れる電流を I2 としますと、
 まったく同じ他の部品にも同じ大きさの電流が流れているはずで、さらに、キルヒホッフ第1法則により抵抗 R には nI2 の電流が流れているはずです。
まったく同じ他の部品にも同じ大きさの電流が流れているはずで、さらに、キルヒホッフ第1法則により抵抗 R には nI2 の電流が流れているはずです。
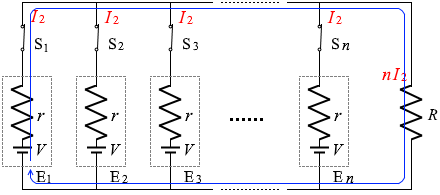 また、左図のような経路についてのキルヒホッフ第2法則の式を立てますと、
また、左図のような経路についてのキルヒホッフ第2法則の式を立てますと、
V = nI2R + I2r
∴ I2 = \(\large{\frac{V}{nR+r}}\)
と I2 が求まります。
よって、電池E1の内部抵抗に発生する単位時間あたりのジュール熱は
\(\large{\frac{Q}{t}}\) = I22r = \(\big(\large{\frac{V}{nR+r}}\big)\small{^2}\large{r}\) = \(\large{\frac{rV^2}{(nR+r)^2}}\)
となります。
(問3)すべてのスイッチS1、S2、…、Sn を閉じた状態で抵抗 R に流れる電流を I とする。n個の電池を図2のように起電力が V で内部抵抗が r' の1個の電池Eに置き換え、抵抗 R に同じ大きさ I の電流が流れるようにしたい。内部抵抗 r' をどのようにとればよいか。
 図 2
図 2
問2で説明したように、抵抗 R に流れる電流は nI2 であり I2 = \(\large{\frac{V}{nR+r}}\) であるから、
I = nI2 = \(\large{\frac{nV}{nR+r}}\)
です。
また、図2におけるキルヒホッフ第2法則の式を立てると、
V = IR + Ir'
であり、これを上式に代入すると、
I = \(\large{\frac{n(IR+Ir')}{nR+r}}\)
∴ 1 = \(\large{\frac{n(R+r')}{nR+r}}\)
∴ nR + r = n(R + r')
∴ r = nr'
∴ r' = \(\large{\frac{r}{n}}\)
と求まります。
5個の電池を1個にする場合には内部抵抗を \(\large{\frac{1}{5}}\)、10個の電池を1個にする場合は内部抵抗を \(\large{\frac{1}{10}}\) にすればいいわけで、これは何となく直感で答えられそうです。
↑
↓


 E1 に流れる電流を
E1 に流れる電流を  まったく同じ部品の E2 にも同じ大きさの電流が流れているはずで、さらに、
まったく同じ部品の E2 にも同じ大きさの電流が流れているはずで、さらに、 また、左図のような経路についての
また、左図のような経路についての
 E1 に流れる電流を
E1 に流れる電流を  まったく同じ他の部品にも同じ大きさの電流が流れているはずで、さらに、キルヒホッフ第1法則により抵抗 R には
まったく同じ他の部品にも同じ大きさの電流が流れているはずで、さらに、キルヒホッフ第1法則により抵抗 R には  また、左図のような経路についてのキルヒホッフ第2法則の式を立てますと、
また、左図のような経路についてのキルヒホッフ第2法則の式を立てますと、