ジュール熱
電荷を運ぶ仕事
『一様な電場での位置エネルギー』で説明したことですが、E [N/C] の電場の中を、q [C] の電荷が、d [m] 進むときの仕事 W [J] は
W = qEd
です。qE の力を受けながら d だけ進むからです。
そして、Ed というのは、電位差 V [V] でもあります。つまり、
W = qV
です。これは、q の電荷が、電位差 V の2点間を進む仕事が qV という意味です。
1ジュール
力学的な仕事の式 W = Fs より、ジュールの単位は [J] = [N⋅m] です。
また、上で示した電磁気的な仕事の式 W = qV より、ジュールの単位は [J] = [C⋅V] です。
つまり、[N⋅m] = [C⋅V] です。
1J という量は、1N の力で 1m 進むようなときの仕事であり、1C の電荷を 1V の電位差分だけ進ませるような仕事でもあります。
重力による位置エネルギーと静電気力による位置エネルギー
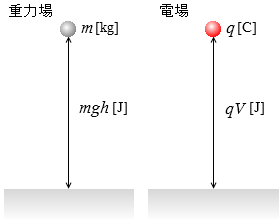重力による位置エネルギーは mgh [J] で、
静電気力による位置エネルギーは qV [J] です。
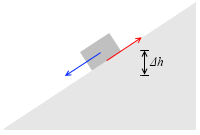m [kg] の物体が摩擦のある斜面を一定の速さで滑り落ちていくとき、位置エネルギーは mgΔh [J] だけ減少します。運動エネルギーは変化しません。速さが一定なので。
このとき、斜面は摩擦によって温められます。発生した熱エネルギーは位置エネルギーの減少分であり、mgΔh [J] です。
ジュール熱
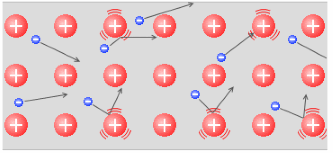導体の両端に電圧を加えると導体内に電場が生じ、自由電子は電場から力を受けて加速します。電流です。加速した自由電子は導体中の他の原子（陽イオン）に衝突し、陽イオンを激しく振動させます。陽イオンというのは自由電子を放出して+の電気を帯びた原子のことです。衝突した自由電子は減速してしまいますが、再び電場から力を受けて加速します。そして陽イオンに衝突し…と、これを繰り返します。自由電子は進みながら陽イオンを振動させるのです。陽イオンが振動するということはこれはつまり熱運動が激しくなるということで、すなわち温度が上がるということです。
このように導体に電流が流れると熱が発生します。そしてこのときの熱をジュール熱といいます。電気ストーブはジュール熱を利用した暖房器具です。
ジュールの法則
抵抗 R [Ω] の導線を電圧 V [V] の電源につなぎ、I [A] の電流を t [s] 間流したとします。
電流というのは I = \(\large{\frac{q}{t}}\) であるから、このときの電荷は q = It [C] です。
電場が電荷を運ぶ仕事 W [J] は W = qV です。ここに上式を代入すると、
W = qV = ItV = IVt
です。これは電場が電荷 q を運んだ仕事であり、電荷が失った位置エネルギーでもあり、これがすべて陽イオンの振動に使われたとしたら、これが導線で発生したジュール熱であるといえます。つまりジュール熱を Q [J]とすると、
Q = IVt
です。位置エネルギーが減った分、ジュール熱が発生するのです。m の物体を h の高さから落とすと mgh の摩擦熱が発生します。
また、 オームの法則 V = RI を用いると、
Q = IVt = I2Rt = \(\large{\frac{\ V^2}{R}}\)t
などと変形することができ、これらをジュールの法則といいます＊19世紀のイギリスの物理学者ジェームズ・プレスコット・ジュール が発見しました。熱の仕事当量を明らかにした人でもあります。
閉じる。
ジュールの法則
Q = IVt = I2Rt = \(\large{\frac{\ V^2}{R}}\)t
もうちょっと詳細に考えてみる
あらためて自由電子の動きまでさかのぼって考え直してみます。
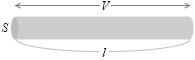断面積 S [m2] 、長さ l [m] 、自由電子の平均の速さ v [m/s] 、自由電子の数密度 n [個/m3] の導線の両端に、V [V] の電圧を掛けたとします。
自由電子は電場の力を受けて加速し、そして陽イオンにぶつかって減速し、トータルで一定のスピードで進んでいくわけです。一定のスピードということは自由電子の運動エネルギーは増えていません。自由電子は電場からエネルギーをもらってそれを全部、陽イオンにあげるのです。陽イオンの振動、つまり熱になるのです。これがジュール熱です。（今は導線について考えているので、自由電子のエネルギーは全部ジュール熱になる、とみなしますが、もしモーターであれば回転エネルギーに変わるし、電球だったら光エネルギーに変わります。）
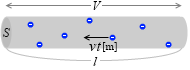個々の自由電子が受ける力は Fe = e\(\large{\frac{V}{l}}\) です。t 秒間に進む距離は vt です。
エネルギーは力×距離なので、この２つを掛け合わせた e\(\large{\frac{V}{l}}\) × vt がエネルギーです。
自由電子の運動エネルギーは変化しないので、このエネルギーはすべて熱エネルギーに変わります。
自由電子の総数、それは nlS 個です。導線の体積 lS [m3] の中に n [個/m3] の数密度で自由電子が存在しているからです。
ですので、熱エネルギーの総量 Q は、
Q = e\(\large{\frac{V}{l}}\) × vt × nlS = eVvtnS = envS × Vt = I × Vt = IVt
であり、これがジュールの法則の式です。