図2のように、抵抗値 10Ω の三つの抵抗、電圧 2.0V の直流電源、スイッチで回路をつくった。ただし、これら三つの抵抗以外の電気抵抗は無視できるものとする。
（問3）次の文中の空欄ア・イに入る数値はいくらか。
スイッチがa側にもb側にも接続されていないとき、OP間の電圧はアV であり、OQ間の電圧はイV である。
（問4）次の文章中の空欄ウ・エに入る数値と語を答えよ。
図2のスイッチをa側に接続すると、回路全体での消費電力 \(P_1\) はウW となる。スイッチをb側に接続すると、回路全体での消費電力 \(P_2\) は \(P_1\) よりエなる。
#センター20本試物理基礎
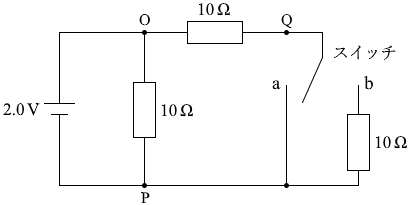
（問3）
スイッチがa側にもb側にも接続されていないなら回路の右半分は無いのと一緒です。
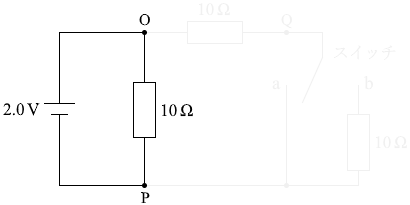ただ単にこのような回路が存在しているのと一緒です。
というわけで、OP間の電圧アは 2.0V で、OQ間の電圧イは 0V です。
（問4）
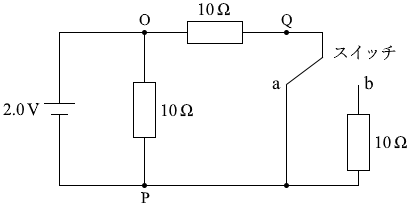スイッチをa側に接続するということは
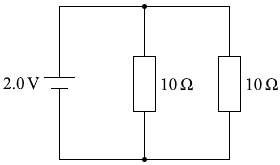このような回路になるということです。
並列の2つの抵抗の合成抵抗を \(R_1\) と置いて求めてみますと、
\({\large\frac{1}{R_1}} = {\large\frac{1}{10}} + {\large\frac{1}{10}}\)
∴ \({\large\frac{1}{R_1}} = {\large\frac{2}{10}}\)
∴ \(R_1\) = 5.0 [Ω]
電圧を抵抗で割って回路を流れる電流の大きさを求めますと、
\({\large\frac{2.0}{5.0}}\) = 0.40 [A]
電流に電圧を掛けて消費電力 \(P_1\) を求めますと、
\(P_1 = 0.40 × 2.0\) = 0.80 [W]
次に、
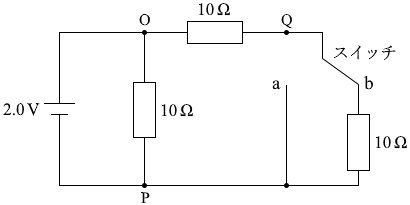スイッチをb側に接続するということは
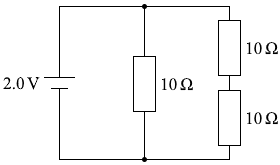このような回路になるということです。
抵抗が増えますので電流が減ります。消費電力は電流と電圧を掛けたものなのでこれも減ります。
消費電力 \(P_2\) は \(P_1\) より 小さく なります。
（いちおう \(P_2\) の数値を求めてみますと）
上記の回路は
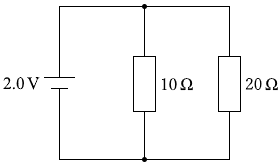（右列は直列接続なので抵抗の大きさは単純に足し合わせることができて）このような回路ということになり、
この並列の2つの抵抗の合成抵抗を \(R_2\) と置いて求めてみますと、
\({\large\frac{1}{R_2}} = {\large\frac{1}{10}} + {\large\frac{1}{20}}\)
∴ \({\large\frac{1}{R_2}} = {\large\frac{3}{20}}\)
∴ \(R_2 = {\large\frac{20}{3}}\) [Ω]
電圧を抵抗で割って電流の大きさを求めますと、
\(2.0 ÷ {\large\frac{20}{3}}\) = 0.30 [A]
電流に電圧を掛けて消費電力 \(P_2\) を求めますと、
\(P_2 = 0.30 × 2.0\) = 0.60 [W]
\(P_1\) = 0.80 [W] より小さくなってます。