直列接続と並列接続

合成抵抗

複数の抵抗をつなげて、それを１つの大きな抵抗とみなしたとき、その抵抗を合成抵抗といいます。

そしてこのとき、抵抗を、直列に接続するか、並列に接続するかによって、合成抵抗の大きさに違いが出ます。

『抵抗率』項で、長さ l を大きくすると抵抗 R が大きくなる、断面積 S を大きくすると抵抗 R が小さくなる、と説明したので、

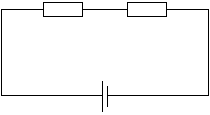直列接続のときは、抵抗の大きさが大きくなり、

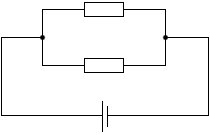並列接続のときは、抵抗の大きさが小さくなると予想がつくと思います。

抵抗の直列接続

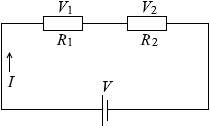左図のように、回路に流れる電流を I [A] 、回路全体の電圧を V [V] 、R₁ [Ω] の抵抗に掛かる電圧を V₁ [V] 、R₂ [Ω] の抵抗に掛かる電圧を V₂ [V] 、全体の合成抵抗を R [Ω] としますと、

回路全体の電圧は V で、電流は I で、抵抗は R なので、オームの法則より、

　　　　V = RI　　……①

R₁ の抵抗にも、R₂ の抵抗にも、同じ I の電流が流れますので、オームの法則より、

　　　　V₁ = R₁I　　V₂ = R₂I　　……②

そして、キルヒホッフの第2法則より、

　　　　V = V₁ + V₂

であるから、この式に①式と②式を代入しますと、

　　　　RI = R₁I + R₂I

　　∴　R = R₁ + R₂

となります。

抵抗の並列接続

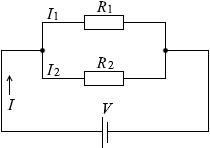左図のように、回路に流れる電流を I [A] 、回路全体の電圧を V [V] 、R₁ [Ω] の抵抗に流れる電流を I₁ [A] 、R₂ [Ω] の抵抗に流れる電流を I₂ [A] 、全体の合成抵抗を R [Ω] としますと、

回路全体の電圧は V で、電流は I で、抵抗は R なので、オームの法則より、

　　　　I = \(\large{\frac{V}{R}}\)　　……③

キルヒホッフの第2法則より、R₁ の抵抗にも、R₂ の抵抗にも、同じ V の電圧が掛かりますので、オームの法則より、

　　　　I₁ = \(\large{\frac{V}{R_1}}\)　　I₂ = \(\large{\frac{V}{R_2}}\)　　……④

そして、キルヒホッフの第1法則より、

　　　　I = I₁ + I₂

であるから、この式に③式と④式を代入しますと、

　　　　\(\large{\frac{V}{R}}\) = \(\large{\frac{V}{R_1}}\) + \(\large{\frac{V}{R_2}}\)

　　∴　\(\large{\frac{1}{R}}\) = \(\large{\frac{1}{R_1}}\) + \(\large{\frac{1}{R_2}}\)

となります。

いろいろな直列接続⋅並列接続

抵抗
　　直列： R = R₁ + R₂
　　並列：\(\frac{1}{R}\) = \(\frac{1}{R_1}\) + \(\frac{1}{R_2}\)

コンデンサー
　　直列：\(\frac{1}{C}\) = \(\frac{1}{C_1}\) + \(\frac{1}{C_2}\)
　　並列： C = C₁ + C₂

ばね
　　直列：\(\frac{1}{K}\) = \(\frac{1}{\ k_1}\)+\(\frac{1}{\ k_2}\)
　　並列： K = k₁ + k₂

回路図における導線の抵抗

電気回路に関して、断っておきたいことがあります。

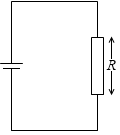回路図においては導線部分には抵抗が無いとみなします。抵抗があるのは抵抗器の部分だけとみなします。

ですので回路図には必ず抵抗器（あるいは抵抗に類する部品）が描かれています。

抵抗の無い回路というのはそれは電源（電池）をショートさせてしまっていることになり、その電気製品は壊れてしまいます。

ゼンマイを一気に解放したらゼンマイが壊れてしまいます。ウェイトトレーニングマシンの重りを一気に落としたらマシンが壊れてしまいます。壊れないためには抵抗が必要です。