オームの法則と電気抵抗
オームの法則
中学理科で、電流と抵抗を掛けると電圧になるというオームの法則というのを習ったと思います。
オームの法則
V = RI
導線の両端の電位差（電圧、電圧降下）が V [V] で、そこに流れる電流が I [A] で、R は電気抵抗と呼ばれる比例定数です。
電気抵抗の単位は [Ω] オーム です＊19世紀のドイツの物理学者ゲオルク・オームから。量記号の R は Resistance（抵抗）から。
閉じる。
このような回路記号を用います。昔は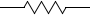 
このような記号を使ってました。
電気抵抗
このオームの法則について、中学理科よりも深く掘り下げて考えてみます。
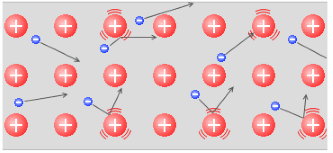電圧を掛けられた自由電子が特定の方向に動いていくのが電流であるわけですが、自由電子は他の原子（陽イオン）にぶつかりながら進むわけです。スムーズに進むわけではありません。これが電気抵抗の原理です。
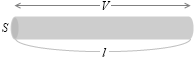断面積 S [m2] 、長さ l [m] 、自由電子の数密度 n [個/m3] の導線の両端に、V [V] の電圧を掛けたとします。
このときに1個の自由電子に掛かる力 Fe [N] は、電場を E [N/C] とすると、
Fe = eE （F = qE であり、1個の自由電子の電気量の大きさは e です）
そして電場 E というのは、
E = \(\large{\frac{V}{l}}\) （V = Ed の d が今は l）
だから、代入すると、
Fe = e\(\large{\frac{V}{l}}\)
となります。自由電子はこのような力を受けて進んでいくのですが、陽イオンにぶつかりながら進むので思うようにスピードは上がりません。抵抗力を受けながら進むのです。この抵抗力は自由電子のスピードが上がれば上がるほど強くなります。これはすなわち進む力と抵抗力が同じになるところでスピードが定まる、ということです。空気抵抗を受ける運動の原理と同じです。
抵抗力は自由電子の平均の速さ v に比例します。そのときの比例定数を k とします。すると抵抗力は kv [N] と表すことができます。
スピードが定まったときというのは、自由電子が進む力 Fe と抵抗力 kv がつり合っているのだから、
e\(\large{\frac{V}{l}}\) = kv
∴ v = \(\large{\frac{eV}{kl}}\)
これを電流の大きさの式の v のところに代入しますと、
I = envS = en\(\bigl(\large{\frac{eV}{kl}}\bigr)\)S = \(\large{\frac{e^2 nSV}{kl}}\) = \(\bigl(\large{\frac{e^2 nS}{kl}}\bigr)\)V
となります。この式のかっこの中の \(\large{\frac{e^2 nS}{kl}}\) の n や S などの各量は、導線の材質や大きさなどを表しています。そして、この部分が大きくなると電流 I が大きくなります。
ここで、このかっこの中の逆数を R と定めますと R = \(\large{\frac{kl}{e^2 nS}}\) となり、R は電流の流れにくさを表していることになります。
この R が電気抵抗と呼ばれる量であり、I = \(\large{\frac{1}{R}}\)V であり、V = RI であり、これがオームの法則です。