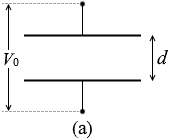
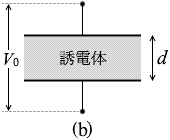
図2(a)に示す極板間隔 d の平行板コンデンサーに、電圧 V0 をかけたときの静電エネルギーを U0 とする。このコンデンサーに図2(b)のように比誘電率 εr の誘電体を極板間にすきまなく挿入し、電圧 V0 をかけた。このとき、極板間の電場の大きさ E と蓄えられた静電エネルギー U を式で表わせ。
#センター16本試物理
図2(a)に示す極板間隔 d の平行板コンデンサーに、電圧 V0 をかけたときの静電エネルギーを U0 とする。このコンデンサーに図2(b)のように比誘電率 εr の誘電体を極板間にすきまなく挿入し、電圧 V0 をかけた。このとき、極板間の電場の大きさ E と蓄えられた静電エネルギー U を式で表わせ。


#センター16本試物理
電場の大きさ E というのは電圧を距離で割ったものであり、誘電体を挿入したからといって電圧も極板間隔も変わらないから、そのままであり、
E = \(\large{\frac{V_0}{d}}\)
また、誘電体を挿入してないときのコンデンサーの電気容量を C0 、誘電体を挿入したときのコンデンサーの電気容量を C' とすると C' = εrC0 であり、
誘電体を挿入してないときの静電エネルギーは
U0 = \(\large{\frac{1}{2}}\)C0V2
誘電体を挿入したときの静電エネルギーは
U = \(\large{\frac{1}{2}}\)C'V2 = \(\large{\frac{1}{2}}\)εrC0V2
U0 と U を見比べると、
U = εrU0
(といいますか、静電エネルギーは電気容量に比例し、電圧の2乗に比例するので、電気容量が εr倍になり、電圧がそのままであれば、静電エネルギーは εr倍になります。)