家庭のコンセントに供給されている電気は交流で、交流は電圧、電流の向きが周期的に変化している。また、交流は変圧器を用いて電圧を変えることができる。
（問2）次の文章中の空欄8⋅9に入る数値はいくらか。
図2(a)のように、電圧を変えられる交流電源と電熱器Rを、長さ 200m の電線2本で接続した。この電線の 1m あたりの抵抗は 2.0×10-4Ω である。電源の電圧を調整して電熱器Rの両端の電圧が 100V になるように設定すると、電熱器Rでの消費電力は 1.0kW となった。このとき、2本の電線で損失する電力 P1 は8W である。
次に、図2(b)のように電熱器Rの直前に変圧器を設置した。変圧器の1次コイルと2次コイルの巻き数比は 20:1 である。交流電源の電圧を大きくし、電熱器Rを電圧 100V 、消費電力 1.0kW で使用したとき、2本の電線で損失する電力 P2 は P1 と比べ9倍になる。ただし、変圧器内部で電力の損失はなく、変圧器によって電圧を変えても、1次コイル側と2次コイル側の電力は等しく保たれるものとする。
#センター14本試
8
2本の電線の抵抗を Ra [Ω] と置きますと、
Ra = 2.0×10-4 × 200 × 2 = 8.0×10-2 [Ω]
電熱器Rの両端の電圧が 100V 、電熱器Rでの消費電力が 1.0kW であるから、電熱器に流れる電流を Ia と置いて電力の式（P = IV）を立てますと、
1.0×103 = Ia × 100
∴ Ia = 10 [A]
この電流は電線部分にも流れますから、電力の式（P = I2R）を立てますと、
P1 = Ia2Ra = 102 × 8.0×10-2 = 8.0 [W]
9
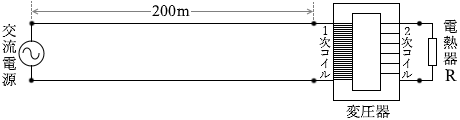
電熱器Rに流れる電流を Ib2 と置いて、上と同じように電力の式を立てて求めますと、
1.0×103 = Ib2 × 100
∴ Ib2 = 10 [A]
これは2次コイルに流れる電流でもあります。そして、変圧器においては電流の比は巻き数の逆比であるから、1次コイルに流れる電流を Ib1 としますと、
Ib1 = \(\large{\frac{1}{20}}\) × Ib2 = \(\large{\frac{1}{20}}\) × 10 = 0.50 [A]
この電流は電線部分にも流れ、電線の抵抗の大きさは8と同じであるから、電力の式（P = I2R）を立てますと、
P2 = Ib12Ra = 0.502 × 8.0×10-2 = 0.25 × 8.0×10-2 [W]
P1 と比べますと、
\(\large{\frac{P_2}{P_1}}\) = \(\large{\frac{0.25×8.0×10^{-2}}{8.0}}\) = 0.25×10-2 = 0.0025 倍
（余談）
図(a)の回路では電線部分で 8.0W の電力が損失し、図(b)の回路では電線部分で 0.25×8.0×10-2 = 0.020W の電力が損失したということです。電線がジュール熱で熱くなったということです。そして、図(b)では電力損失が\(\large{\frac{1}{400}}\)に抑えられたということです。
変圧器において、電圧の比は巻き数の比であるので、図(b)の回路において1次コイル側の電圧は 100[V]×20 = 2000[V] ということになります。高電圧で送電すると電力損失が少なく、効率がいいのです。このことは『変圧器_補足』項で説明しました。