変圧器

変圧器は交流でのみ使える 基礎物理範囲

相互誘導現象を利用すると、交流の電圧を容易に変化させることができます。その装置を変圧器といいます。直流に関しては、電流が一定なので相互誘導が起こらず、変圧器を用いても電圧を変化させることはできません。

誘導起電力の比 物理範囲

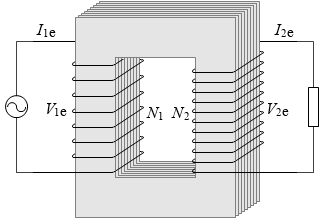1次コイル、2次コイルに流れる電流をそれぞれ I_1e [A] ＊いま考えてる電流は交流ですのでその値は実効値であるとし、量記号に _e の添字を付けることにします。
　閉じる、I_2e [A] とし、電圧をそれぞれ V_1e [V] 、V_2e [V] とし、コイルの巻き数をそれぞれ N₁ 、N₂ とし、コイルを貫く磁束を Φ [Wb] とします。

は交流電源のマークです。

＊変圧器に用いられる鉄心は大抵の場合、板状のものを重ね合わせてミルフィーユ状にしてあります。

鉄心に磁束が通ると渦電流が発生しますが、


鉄心がスライスしてあれば渦電流を小さくすることができ、余分な発熱を抑えられます。

　閉じる

1次コイルに V_1e の電圧を掛けると I_1e の電流が流れ、磁束 Φ が変化します。理想的な鉄心であれば2次コイルでも同じだけ磁束 Φ が変化し、V_2e の相互誘導起電力が発生します。式で書くと以下のようになります。

　　　　V_1e = - N₁\(\large{\frac{ΔΦ}{Δt}}\)　　　　（『自己インダクタンス』参照）

　　　　V_2e = - N₂\(\large{\frac{ΔΦ}{Δt}}\)　　　　（『環状鉄心の相互インダクタンス』参照）

この2式は - \(\large{\frac{ΔΦ}{Δt}}\) という値が共通しています。上式を下式で割りますと、

　　　　\(\large{\frac{V_{1\rm{e}}}{V_{2\rm{e}}}}\) = \(\large{\frac{N_1}{N_2}}\)

となります。1次コイルと2次コイルの電圧の比は巻き数の比と等しくなっています。この原理を用いることによって、交流の電圧は自在に上げ下げすることができます。電圧を2倍にしたければ巻き数を2倍にすればいいのです。

磁束が等しい 物理範囲

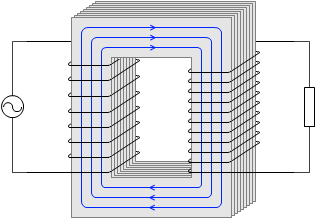このことが成り立つのはあくまでも双方のコイルの磁束 Φ が一致しているときです。

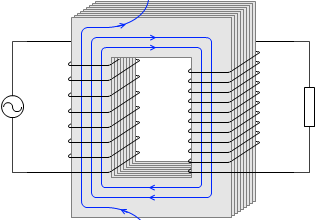磁束が漏れているようなときは成り立ちません。

電流の比 基礎物理範囲

もし、磁束の漏れもなく、（上図においては右側の）抵抗器部分以外においてジュール熱も発生しないとすると、エネルギー保存の法則より、1次コイルと2次コイルの電力は等しくなっていて、

　　　　I_1eV_1e = I_2eV_2e

が成り立っています。これは変形すると、

　　　　\(\large{\frac{V_{1\rm{e}}}{V_{2\rm{e}}}}\) = \(\large{\frac{I_{2\rm{e}}}{I_{1\rm{e}}}}\)　　　（1と2の対応が逆になってます）

とも表せます。

電圧を2倍にしようとして巻き数を2倍にすると電流は半分になります。

まとめ 基礎物理範囲

これは以下のように表現することもできます。

　　　　V_1e : V_2e = I_2e : I_1e = N₁ : N₂

　　　　I_1eV_1e = I_2eV_2e