qHBN7　■わかりやすい高校物理の部屋■

変圧器と送電について考える。

（問3）変圧器において、1次コイルの巻数 N₁ と2次コイルの巻数 N₂ の比が N₁ : N₂ = 10 : 1 の場合、1次コイル側に 100V の交流電圧を加えたとき、 2次コイル側の電圧は何V か。

（問4）次の文章中の空欄ア〜ウに入れる式と語の組合せとして最も適当なものを、下の①～⑧のうちから一つ選べ。

　発電所から送電線に送り出される交流の電圧を V 、電流を I とすると、その電力はアと表される。送電線の抵抗値が R であるとき、送電線で消費される電力は、イとなる。したがって、同じ電力量を送るとき、送電線での電力損失を小さくするには、発電所で変圧器を使い、電圧をウして送電すればよい。

	①	②	③	④	⑤	⑥	⑦	⑧
ア	\(\large{\frac{V}{I}}\)	\(\large{\frac{V}{I}}\)	\(\large{\frac{V}{I}}\)	\(\large{\frac{V}{I}}\)	`IV`	`IV`	`IV`	`IV`
イ	\(\large{\frac{\ V^2}{R}}\)	\(\large{\frac{\ V^2}{R}}\)	`I`²`R`	`I`²`R`	\(\large{\frac{\ V^2}{R}}\)	\(\large{\frac{\ V^2}{R}}\)	`I`²`R`	`I`²`R`
ウ	低く	高く	低く	高く	低く	高く	低く	高く

#センター16本試物理基礎

（問3）
変圧器において巻数の比は電圧の比であるので、

　　　　N₁ : N₂ = 10 : 1 = 100 : 10

答えは 10V 。

（問4）
この問題の内容は『変圧器_補足』項で詳しく説明しましたが、その項を読んでいない方は問題の意図がさっぱり分からないと思います。

ポイントは、
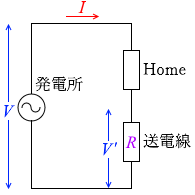各家庭と送電線は直列につながれていて、電流の大きさは共通だが電圧は違う、というところです。

「　発電所から送電線に送り出される交流の電圧を V 、電流を I とすると、その電力は IV と表される。送電線の抵抗値が R であるとき、送電線で消費される電力は、 I²R となる（または\(\large{\frac{\ \color{#00f}{V'^2}}{\color{#c0c}{R}}}\) となる。\(\large{\frac{\ \color{#00f}{V^2}}{\color{#c0c}{R}}}\)ではない）。したがって、同じ電力量を送るとき、送電線での電力損失を小さくするには、発電所で変圧器を使い、電圧を高くして送電すればよい。（なぜなら電力量が同じということは電力が同じということであり、電力は IV であり、これが同じということは V を高くすれば I が小さくなり、送電線での損失 I²R が小さくなるから。）　」

答えは ⑧ です。

『変圧器_補足』項を読み直してみてください。V-Iグラフの青面積をいかに大きく、緑面積をいかに小さくするか、というのが本問の主旨です。