(問1)
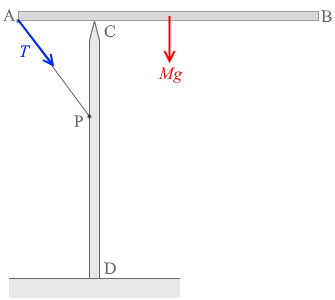 糸の張力を T 、棒ABの質量を Mとしますと、棒に及ぼす力のうち分かっているものは左図のような T と Mg です(一様な棒の重心はその中点にあります。)。
糸の張力を T 、棒ABの質量を Mとしますと、棒に及ぼす力のうち分かっているものは左図のような T と Mg です(一様な棒の重心はその中点にあります。)。
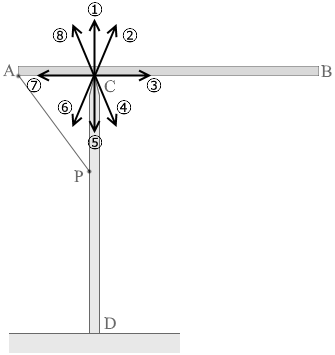
あともう一つの力は点Cからの力であり、棒ABが動かないためには、これは上向きの力であるはずです。
そして、張力 T が若干右を向いてますので、点Cからの力はちょっと左を向いているはずです。
というわけで点Cから棒ABに及ぼす力の方向として最適なのは ⑧ です。
(余談)
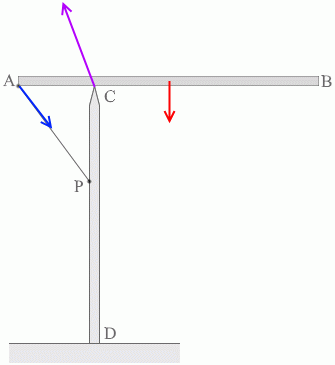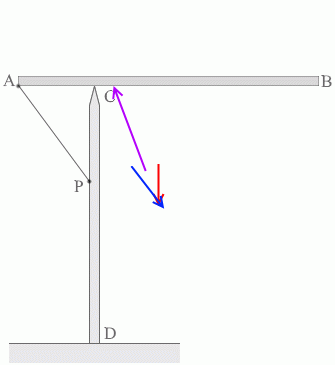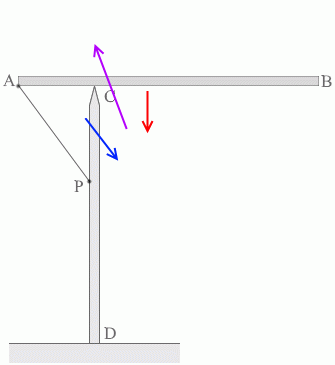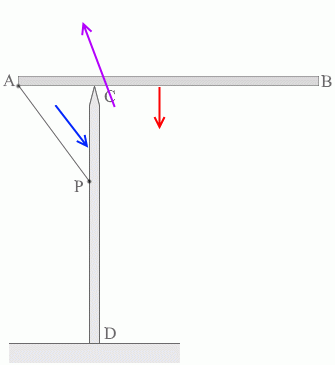 棒ABに掛かる3つの力は、合わせると 0 になりますし、数珠つなぎにすると閉じた三角形ができます。
棒ABに掛かる3つの力は、合わせると 0 になりますし、数珠つなぎにすると閉じた三角形ができます。
(問2)
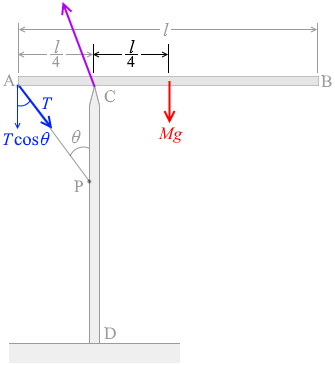 点Cの回りの力のモーメントのつり合いを考えます。
点Cの回りの力のモーメントのつり合いを考えます。
Mg の位置は点Cから \(\large{\frac{l}{4}}\) です。
張力 T の点Cに対する垂直成分は Tcosθ です。
力のモーメントは(力の垂直成分)×(腕の長さ) ですから、力のモーメントのつり合いの式は
Tcosθ × \(\large{\frac{l}{4}}\) = Mg × \(\large{\frac{l}{4}}\)
であり、
∴ Tcosθ = Mg
∴ T = \(\large{\frac{Mg}{\cosθ}}\)
と求められます。
(余談)
ここまで求まると、紫の矢印の力(Fc)の大きさも求まります。鉛直成分と垂直成分に分けて、力のつり合いを考えます。
Fc の鉛直成分 = Tcosθ + Mg = Mg + Mg = 2Mg
Fc の水平成分 = Tsinθ = \(\large{\frac{Mg}{\cosθ}}\)sinθ = Mgtanθ
ここから三平方の定理を用いれば Fc の大きさが求まります。
また、もしAC間の距離がもっと小さくて \(\large{\frac{l}{8}}\) だったりしたら、上の
Tcosθ × \(\large{\frac{l}{4}}\) = Mg × \(\large{\frac{l}{4}}\)
の式が
Tcosθ × \(\large{\frac{l}{8}}\) = Mg × \(\large{\frac{3}{8}}\)l
となり、T や Fc がとても大きくなります。テコの原理です。
逆に、AC間の距離が \(\large{\frac{l}{2}}\) だったりしたら T は 0 となります。
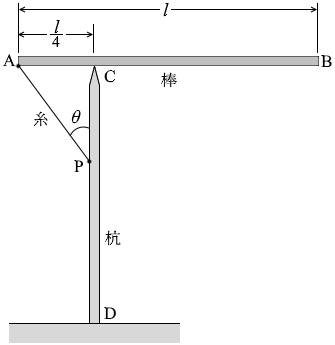
 糸の張力を T 、棒ABの質量を Mとしますと、棒に及ぼす力のうち分かっているものは左図のような
糸の張力を T 、棒ABの質量を Mとしますと、棒に及ぼす力のうち分かっているものは左図のような  棒ABに掛かる3つの力は、合わせると 0 になりますし、数珠つなぎにすると閉じた三角形が
棒ABに掛かる3つの力は、合わせると 0 になりますし、数珠つなぎにすると閉じた三角形が 点Cの回りの
点Cの回りの