質量 m のかたくて一様な筒ABがある。この筒は両端が開いており、図3のようにABの間Cに仕切りがある。AC、CBの長さは、それぞれ l1 、 l2 である。筒は十分細長く、仕切りの質量は無視できるとする。
（問4）この筒を点A、B、Cを含む鉛直面内でなめらかに回転できるように、Cを支点として支えたところ、図4のように端Aが床に接した。このとき、端Aおよび支点Cで、筒が鉛直上向きに受けている力の大きさはそれぞれいくらか。ただし、重力加速度の大きさを g とし、床はなめらかとする。
（問5）仕切りで区切られた筒のCBの部分には水をためることができる。ちょうど端Bまで水で満たされたとき筒が回転を始めるようにしたい。筒の断面積を S 、水の密度を ρ とするとき、l1 と l2 の関係を示せ。
#センター00本試
（問4）
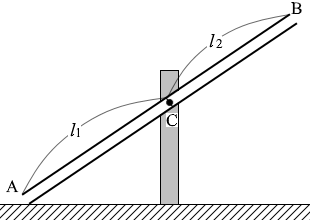
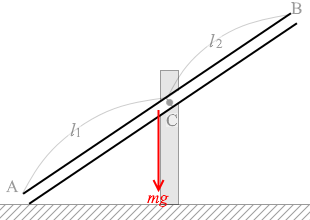一様な筒の重心はその中点にあります。
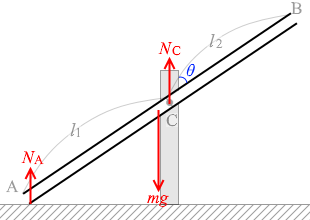その筒の重さを点Aと点Cの2点で支えています。
それぞれの力の大きさを NA 、NC 、筒とのなす角を θ と置きます。
筒は静止しているので力のモーメントはつり合っています。
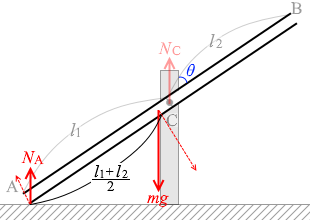点Cのまわりの力のモーメントのつり合いを考えますと、
NC は腕の長さが 0 です。
NAsinθ × l1 = mgsinθ × ( l1 - \(\large{\frac{l_1+l_2}{2}}\) )
∴ NA × l1 = mg × ( l1 - \(\large{\frac{l_1+l_2}{2}}\) )
∴ NA × l1 = mg × ( \(\large{\frac{2l_1-l_1-l_2}{2}}\) )
∴ NA × l1 = mg × ( \(\large{\frac{l_1-l_2}{2}}\) )
∴ NA × l1 = \(\large{\frac{1}{2}}\)mg × ( l1 - l2 )
∴ NA = \(\large{\frac{1}{2}}\)mg( 1 - \(\large{\frac{l_2}{l_1}}\) )
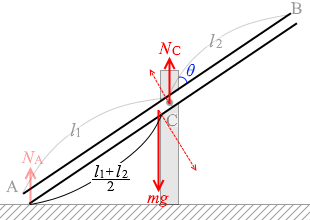点Aのまわりの力のモーメントのつり合いを考えますと、
NCsinθ × l1 = mgsinθ × \(\large{\frac{l_1+l_2}{2}}\)
∴ NC × l1 = mg × \(\large{\frac{l_1+l_2}{2}}\)
∴ NC × l1 = \(\large{\frac{1}{2}}\)mg × ( l1 + l2 )
∴ NC = \(\large{\frac{1}{2}}\)mg( 1 + \(\large{\frac{l_2}{l_1}}\) )
（あるいは）
力のモーメントのつり合いではなく、鉛直方向の力のつり合いを考えますと、mg = NA + NC だから、
NC = mg - NA
= mg - \(\large{\frac{1}{2}}\)mg( 1 - \(\large{\frac{l_2}{l_1}}\) )
= mg - \(\large{\frac{1}{2}}\)mg + \(\large{\frac{1}{2}}\)mg\(\large{\frac{l_2}{l_1}}\)
= \(\large{\frac{1}{2}}\)mg + \(\large{\frac{1}{2}}\)mg\(\large{\frac{l_2}{l_1}}\)
= \(\large{\frac{1}{2}}\)mg( 1 + \(\large{\frac{l_2}{l_1}}\) )
（余談）
NA の式にも NC の式にも θ が出てきませんので、角度は無関係（つまり支柱の高さは無関係）と分かります。
また、l1 = l2 のとき、NA = 0 、NC = mg です。さらに、l1 : l2 = 1000 : 1 のとき、NA ≒ NC ≒ \(\large{\frac{1}{2}}\)mg となります。
（問5）仕切りで区切られた筒のCBの部分には水をためることができる。ちょうど端Bまで水で満たされたとき筒が回転を始めるようにしたい。筒の断面積を S 、水の密度を ρ とするとき、l1 と l2 の関係を示せ。
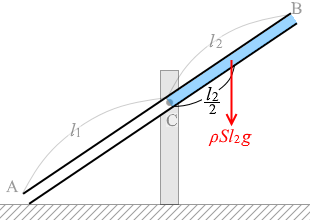CB部分の体積は Sl2 であり、水を満たしたときのその重さは ρSl2g であり、重心はその中点にあります。
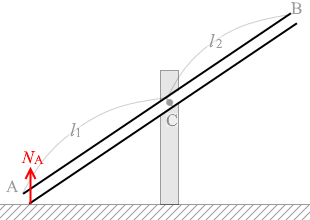筒が回転を始める瞬間というのは、端Aが浮き始めるということであり、浮き始めるということは鉛直上向きの効力が 0 になるということです。
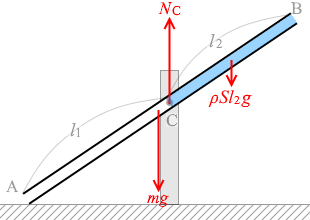ということは、筒に掛かる力は左図のような3つになります。
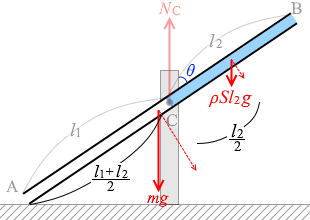点Cのまわりの力のモーメントのつり合いを考えますと、
mgsinθ × ( l1 - \(\large{\frac{l_1+l_2}{2}}\) ) = ρSl2g sinθ × \(\large{\frac{l_2}{2}}\)
∴ m × ( l1 - \(\large{\frac{l_1+l_2}{2}}\) ) = ρSl2 × \(\large{\frac{l_2}{2}}\)
∴ m × ( \(\large{\frac{2l_1-l_1-l_2}{2}}\) ) = ρSl2 × \(\large{\frac{l_2}{2}}\)
∴ m × ( \(\large{\frac{l_1-l_2}{2}}\) ) = ρSl2 × \(\large{\frac{l_2}{2}}\)
∴ m × ( l1 - l2 ) = ρSl2 × l2
∴ ( l1 - l2 ) = \(\large{\frac{1}{m}}\)ρSl2 × l2
∴ l1 = l2 + \(\large{\frac{1}{m}}\)ρSl22
（余談）
この式はシシオドシ（➚Wikipedia）の設計に役立ちます。l2 が短すぎたり、筒の質量 m が大きすぎたりすると、目一杯水を入れても筒が回転せず、シシオドシの音が鳴りません。
あと細かい話ですが、
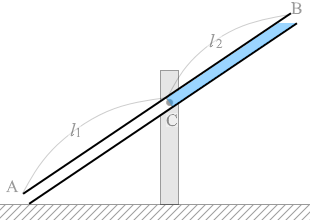水はこのように溜まるはずですが、このことは無視します。そのためにわざわざ問題文に「筒は十分細長く、」と書いてあります。