qGACH

棒は静止しているので、剛体にはたらく力のつり合いの条件

　　\(\vec{F}_1\) + \(\vec{F}_2\) + \(\vec{F}_3\) + … = 0　……①

　　M₁ + M₂ + M₃ + … = 0　……②

が成り立っています。①は（問1）qGACF のことです。（問3）で問われているのは②です。②式により点Pの位置が特定できます。

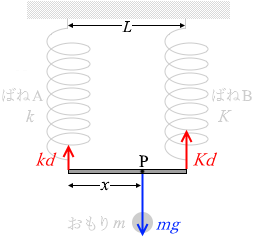求める距離を x 、右回りを正、点Pを中心として②式を立てますと、

　　kd×x + mg×0 - Kd×(L - x) = 0

∴　kdx - KdL + Kdx = 0

∴　kx - KL + Kx = 0

∴　(k + K)x = KL

∴　x = \(\large{\frac{K}{k+K}}\)L

（余談）
点Pの左側の長さと点Pの右側の長さの比は

　　　　x : (L - x) = \(\large{\frac{K}{k+K}}\)L : (L - \(\large{\frac{K}{k+K}}\)L)

　　　　　　　　　= \(\large{\frac{K}{k+K}}\) : (1 - \(\large{\frac{K}{k+K}}\))

　　　　　　　　　= \(\large{\frac{K}{k+K}}\) : (\(\large{\frac{k+K}{k+K}}\) - \(\large{\frac{K}{k+K}}\))

　　　　　　　　　= \(\large{\frac{K}{k+K}}\) : \(\large{\frac{k}{k+K}}\)

　　　　　　　　　= K : k

であり、点Pの位置はばね定数の逆比であり強いばねの方に寄ります。