図2のように、質量 m で長さ L の一様な細い棒を、壁に斜めに立てかけたところ、棒はすべらず静止した。壁はなめらかでかつ鉛直であり、床はあらくかつ水平である。また棒が床となす角度を θ とする。そこに、質量 \(\large{\frac{m}{3}}\) の小鳥が飛んできて棒上の一点に静かにとまったが、棒は静止したままであった。棒の太さと小鳥の大きさは無視できるものとし、重力加速度の大きさを g とする。
（問3）小鳥が棒の上端から距離 x の点にとまったとき、小鳥と棒を合わせた重心の位置が、棒の上端から距離 \(\large{\frac{2}{5}}\)L の点になった。x はいくらか。
（問4）床と棒の間の静止摩擦係数を μ とする。問3の位置に小鳥がとまった後も棒がすべり出さないための μ の最小値 μ0 はいくらか。
#センター09追試
（問3）
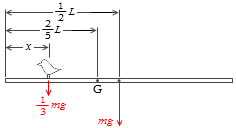
重心というものはその物体にただ1箇所だけ存在するものであり、物体の向きを変えても重心の位置は変わりません。ですので、考えやすいように、棒を水平にして考えます。
棒 mg
一様な棒の単体の重心はその中点にあります。
と小鳥 \(\large{\frac{1}{3}}\)mg の重心が点Gということです。
xG = \(\large{\frac{m_1x_1\ +\ m_2x_2}{m_1\ +\ m_2}}\)
に当てはめて x を求めますと、
\(\large{\frac{2}{5}}\)L = \(\large{\frac{\frac{1}{3}mx\ +\ m\frac{1}{2}L}{\frac{1}{3}m\ +\ m}}\)
∴ \(\large{\frac{2}{5}}\)L = \(\large{\frac{\frac{1}{3}x\ +\ \frac{1}{2}L}{\frac{1}{3}\ +\ 1}}\)
∴ \(\large{\frac{2}{5}}\)L × \(\large{\frac{4}{3}}\) = \(\large{\frac{1}{3}}\)x + \(\large{\frac{1}{2}}\)L 両辺に 30 を掛けて
∴ 16L = 10x + 15L
∴ 10x = 16L - 15L
∴ x = \(\large{\frac{1}{10}}\)L
（問4）
図2を、小鳥の質量を付け足し、少し移動した重心の位置を考慮して、あらためて描き直すと次のようになります。
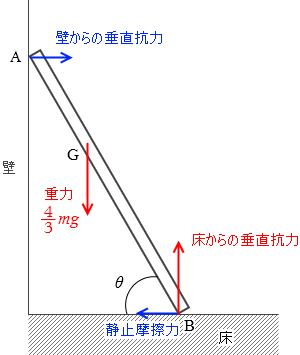
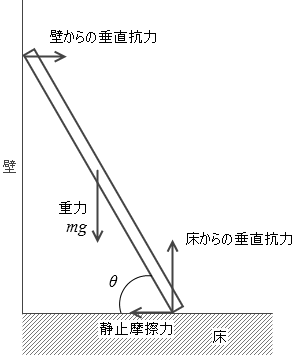
棒が動かず静止しているということは、
(1) 重力と床からの垂直抗力がつり合っている
(2) 壁からの垂直抗力と静止摩擦力がつり合っている
(3) 4つの力のモーメントがつり合っている
(1)より、床からの垂直抗力は \(\large{\frac{4}{3}}\)mg
また、最大静止摩擦力は摩擦係数と垂直抗力を掛けたもので μ\(\large{\frac{4}{3}}\)mg でありますが、静止摩擦力は μ\(\large{\frac{4}{3}}\)mg 以下の何かしらの値です。
摩擦係数が μ0 であれば、最大静止摩擦力は μ0\(\large{\frac{4}{3}}\)mg であり、これは、すべり出すかどうかぎりぎりのときの静止摩擦力のことでもあります。
(2)より、この力と壁からの垂直抗力がつり合っているのだから、壁からの垂直抗力の大きさは μ0\(\large{\frac{4}{3}}\)mg
次に、(3)について考えますが、
力のモーメントのつり合いについては、力のモーメントの中心はどこに設定してもいいので、上図の点Bを中心として考えることにします。そうすると、床からの垂直抗力と静止摩擦力は考えなくてよくなります。腕の長さが 0 になるからです。
B点のまわりの力のモーメントのつり合いの式は、右回りを正として、（qG931、qG6Q1参照）
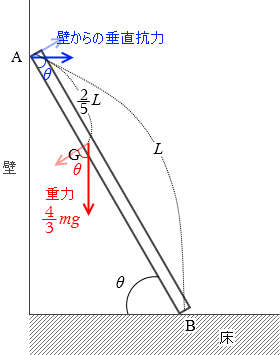
壁からの垂直抗力 × sinθ × L - 重力 × cosθ × \(\large{\frac{3}{5}}\)L = 0
⇔ μ0\(\large{\frac{4}{3}}\)mg × sinθ × L - \(\large{\frac{4}{3}}\)mg × cosθ × \(\large{\frac{3}{5}}\)L = 0
∴ μ0\(\large{\frac{4}{3}}\)mgLsinθ - \(\large{\frac{4}{3}}\)×\(\large{\frac{3}{5}}\)mgLcosθ = 0
∴ μ0sinθ - \(\large{\frac{3}{5}}\)cosθ = 0
∴ μ0sinθ = \(\large{\frac{3}{5}}\)cosθ
∴ μ0 = \(\large{\frac{3}{5}\frac{\cosθ}{\sinθ}}\) = \(\large{\frac{3}{5\tanθ}}\)
μ0 ではなく μ を用いて立式したい場合は、
棒が左に回転してしまわないための条件式を立てます。
μ\(\large{\frac{4}{3}}\)mg × sinθ × L ≧ \(\large{\frac{4}{3}}\)mg × cosθ × \(\large{\frac{3}{5}}\)L
・
・
・
μ ≧ \(\large{\frac{3}{5\tanθ}}\)
μ = \(\large{\frac{2.9}{5\tanθ}}\) ではすべってしまって、μ = \(\large{\frac{3}{5\tanθ}}\) では大丈夫で、μ = \(\large{\frac{3.1}{5\tanθ}}\) でも大丈夫ということです。最小の値が \(\large{\frac{3}{5\tanθ}}\) ということです。