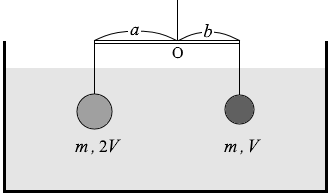
軽い棒の両端に二つのおもりを軽くて細い糸でつなぎ、両方のおもりを密度 ρ の液体中に沈めた。図5のように、棒を点Oでつるしたところ、すべての糸はたるむことなく、棒は水平になって静止した。左右のおもりの質量はともに m であり、体積はそれぞれ 2V 、V である。点Oから棒の左端までの距離 a と、点Oから棒の右端までの距離 b の比 \(\large{\frac{a}{b}}\) を式で表せ。
#センター13本試
軽い棒の両端に二つのおもりを軽くて細い糸でつなぎ、両方のおもりを密度 ρ の液体中に沈めた。図5のように、棒を点Oでつるしたところ、すべての糸はたるむことなく、棒は水平になって静止した。左右のおもりの質量はともに m であり、体積はそれぞれ 2V 、V である。点Oから棒の左端までの距離 a と、点Oから棒の右端までの距離 b の比 \(\large{\frac{a}{b}}\) を式で表せ。
#センター13本試
重力加速度の大きさを g としますと、
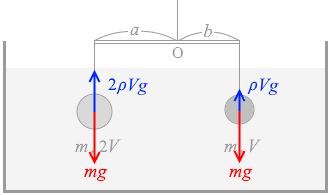左のおもりには mg の重力と 2ρVg の浮力がはたらいていて、
右のおもりには mg の重力と ρVg の浮力がはたらいています。
a、b の長さの比は、左端、右端に掛かる重さの逆比だから、
丁寧にいえば、
静止しているのだから力のモーメントの和は 0 のはずであり、
(mg - 2ρVg)×a - (mg - ρVg)×b = 0
\(\large{\frac{a}{b}}\) = \(\large{\frac{mg-ρVg}{mg-2ρVg}}\) = \(\large{\frac{m-ρV}{m-2ρV}} \)