浮力

浮力の式

船が海に浮いたり、プールに入ると体が軽く感じたり、池に投げた石がゆっくり沈んでいくのは、水の中に浮き上がらせようとする力があるからです。この力を浮力といいます。

水中の物体の、上面を押す力より下面を押す力の方が大きいことにより、浮力が生じます。流体中では深さによって圧力が違いますが、この圧力差によって生じる鉛直上向きの力が浮力です。

浮力の式を導出してみます。

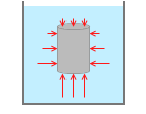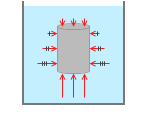左図のような物体が水中にあるとします。物体の側面にはたらく圧力は対面同士でつり合うので合力は 0 です。

物体の上面を押す圧力を p₁ [Pa]、下面を押す圧力を p₂ [Pa]、上面の深さを h₁ [m]、下面の深さを h₂ [m]、大気圧を p₀ [Pa]、水の密度を ρ [kg/m³]、物体の体積を V [m³]、上面、下面の面積を S [m²]、高さを l [m]、とします。

流体の圧力の式　p = p₀ + ρhg　に代入しますと、

　　物体の上面を押す圧力： p₁ = p₀ + ρh₁g

　　物体の下面を押す圧力： p₂ = p₀ + ρh₂g

浮力 = 下面を押す力 - 上面を押す力 、ですから、浮力を F [N] とすると、

　　F = p₂×S - p₁×S
　　　= { p₂ - p₁ }×S
　　　= {(p₀ + ρh₂g) - (p₀ + ρh₁g)}×S
　　　= {ρh₂g - ρh₁g}×S
　　　= {h₂ - h₁}×ρgS
　　　= l×ρgS
　　　= ρ(lS)g
　　　= ρVg

となります。

この式は水だけでなく他の流体でも成り立ちます。

そしてよく見ますと、物体の密度を表す記号が含まれていません。流体の密度を表す記号は含まれています。浮力は、物体の密度とは無関係で、流体の密度とは関係があるのです。（下で説明する『浮き沈み』については物体の密度も流体の密度も両方関係します）。
その他に関係するのは物体の体積だけです。（ g は定数です）。
深さも関係ありません。（水圧は深さが関係します）。
大気圧も関係ありません。

アルキメデスの原理

上式を解釈しますと、浮力の大きさは流体の密度と物体の体積を掛け合わせたものに g を掛けたもの、となります。

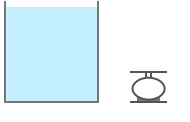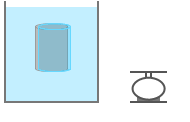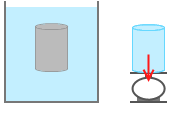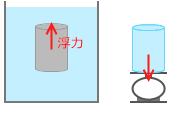これは、物体が排除した流体の重さ、と言い換えることもできます。

これをアルキメデスの原理といいます＊紀元前3世紀のギリシアの数学者、アルキメデスが発見しました。
　閉じる。

これを水圧の項と同じように微視的に説明してみます。

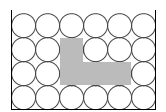左図は水分子の中に物体が沈められている場面を例示しています。これはあくまでも説明のための仮想モデルです。

この物体に掛かる圧力は、

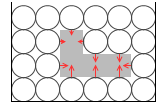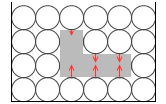このようになります。

横方向の圧力はちょうど対面同士で打ち消し合います。縦方向の圧力だけ残ります。

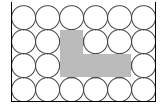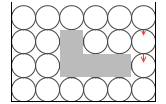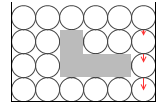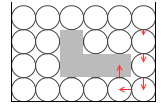このときの下面を突き上げる力というのは、周りの分子たちの力が潜り込むことによって生まれるものです。『パスカルの原理』項、『水圧の原理』項を読んでみてください。それでもわからないという方は「球体による潜り込み効果によって上方向にも力が伝わる」と覚えてください。

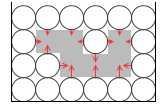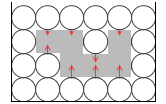どのような形の物体でも、横方向の圧力は対面同士で打ち消し合い、縦方向の圧力だけ残ります。浮力の方向が常に鉛直上向きであるゆえんです。

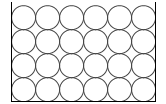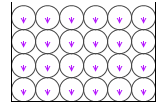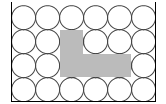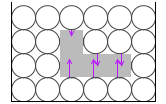
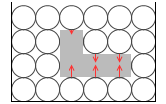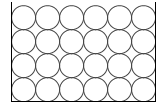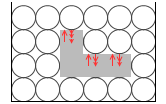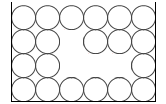残った縦方向の圧力を見ますと、その圧力差は分子の個数分になります。左図では分子4個分です。段数によって圧力に差があるのは分子自身の重さによるものだからです。

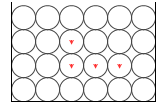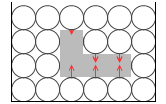
左図の赤矢印から紫矢印のように、分子が重いものに変わる（密度が大きくなる。たとえば真水から塩水に変わる）と矢印の長さの差も大きくなるので、物体に掛かる圧力差も大きくなります。

というわけで、物体の上面と下面を押す力の差（＝浮力）は、（分子の個数）×（分子の重さ）となります。これはまさに物体が排除した流体の重さであり、これがアルキメデスの原理であります。

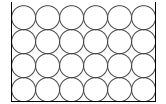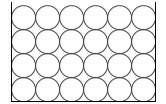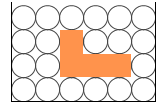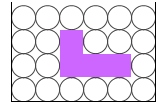
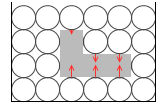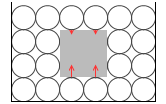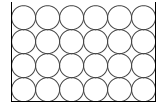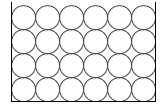体積が同じならば、物体の向きが変わっても物体の形が変わっても、浮力の大きさは変わりません。左図においては、どのように変化しようと、浮力は分子4個分の重さです。

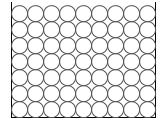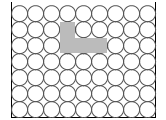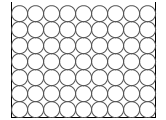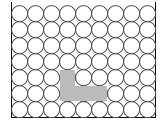体積が同じならば、深いところにあっても浅いところにあっても、浮力の大きさは変わりません。左図においては、物体が浅いところにあろうと深いところにあろうと、浮力は分子4個分の重さです。

物体の材質（密度）が変わっても、その体積が変わらなければ、浮力も変わりません。

浮き沈み

体積が変わらなければ浮力は変わりませんが、物体の密度が変われば浮くかもしれないし沈むかもしれません。物体が浮くか沈むかは、浮かせようとする力（浮力）と沈ませようとする力の兼ね合いで決まります。浮き沈みは浮力だけでは決まりません。

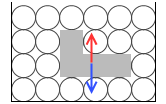物体の体積は変わらないとして、物体が重くなる（物体の密度が大きくなる）と沈ませようとする力は大きくなります。この力が浮力より大きいか小さいかで物体が浮くか沈むか決まります。

いま下向きを正と決めますと、

　　沈ませようとする力 - 浮力 = 合力

という式が書けます。この式における合力が +（プラス）なら物体は沈みますし -（マイナス）なら物体は浮きます。この合力と浮力を混同しないようにしてください。

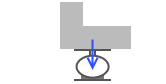このとき、沈ませようとする力というのは物体の重さであります。

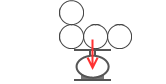浮力というのは物体が排除した流体の重さを上向きに変えたものです。

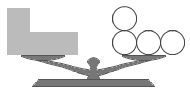この2つは体積が同じです。
ということは、この2つの重さを比べるということは、この2つの物質の密度（単位体積当たりの質量）を比べるということです。つまり、合力がプラスかマイナスかを調べることは、物体の密度と流体の密度を比較するということになります。

いま、流体の密度が 1000 kg/m³（水）で一定であるとします。
物体の密度がこれと同じ 1000 kg/m³ であるならば、物体は水中で静止します。物体の密度がこれより大きければ、物体は沈みます。物体の密度がこれより小さければ、物体は浮きます。

今度は、物体の密度が 1000 kg/m³ で一定であるとします。
流体の密度がこれと同じ 1000 kg/m³ であるならば、物体は静止します。流体の密度がこれより大きければ（海水など）、物体は浮きます。流体の密度がこれより小さければ（油など）、物体は沈みます。

プールの水より海水の方が体が浮きやすいのは、真水より海水の方が密度が大きいからです。

上の例は、体積を考えず密度だけを比較すればいいという例でしたが、密度が均一でない物体の場合は、物体全体の体積と物体全体の重さを考えなければなりません。物体の体積が大きければ排除する流体の量も大きくなるのだから浮力も増しますし、物体の重さが大きくなれば沈ませようとする力が大きくなります。その兼ね合いで浮くか沈むかが決まります。

潜水艦は、海中に留まっているときは、浮力と沈ませようとする力の合力が 0 になるように調整されています。
沈もうとするときは、バラストタンクといわれる装置に海水をいれて潜水艦全体の体積を減らして、浮力を小さくして沈みます。（これは海水を入れて潜水艦を重くして沈ませようとする力を大きくしたとみなすこともできます）。
浮上するときは、バラストタンクから海水を吐き出して潜水艦全体の体積を増やして、浮力を大きくして浮上します。（これは潜水艦の重さを軽くしたともみなせます）。

人間も、息を吸って肺を膨らまして体積を増やすと浮きやすいですし、息を吐いて肺を小さくして体積を小さくすると潜水しやすいです。

タンカーは、浮力と沈ませようとする力の合力が 0 になって一定の高さを保っているわけですが、港で荷物を降ろすとタンカーの総重量が軽くなり（すなわち沈ませようとする力が小さくなり）浮力が勝り、浮き上がります。だんだん浮き上がっていくと、タンカーの海水に沈んでいる部分の体積が小さくなり（すなわち排除する流体の量が小さくなり）浮力が小さくなっていき、沈ませようとする力とつり合って（合力が 0 になって）静止します。タンカーは荷物を積んでいるときと積んでいないときで高さがだいぶ違います。それでも違いすぎると困るので、潜水艦と同様、バラストタンクが備わっているそうです。

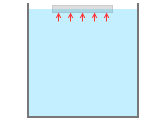なお、水面に浮かんでいるものには浮力がはたらかない、と勘違いしないでください。浮力というのは物体の上面を押す力と下面を押す力の差のことでありますが、上面から押す力がなくても下面から押す力があるので、浮力はあります。水面に浮かんでいる板においても、わずかに沈んでいる部分によって流体を排除していますので浮力が発生しています。そして浮かび続けているということは、沈ませようとしても浮力の方が勝ってしまうということであり、これはすなわち物体の密度が流体の密度より小さいということです。

軽い物体が水底にある場合

また、水よりも密度の小さい（＝軽い）物体が水底にある場合、浮力がはたらいて上昇するのかどうか、という問題がありますが、この問題を額面どおりに受け止めれば、浮力ははたらかない、ということになります。物体の下に水が入り込まないと浮力ははたらかないからです。しかし実際には、物体の下の隙間に水が入り込んで浮力がはたらいて物体は上昇してしまいます。物体を上昇させないためには吸盤のようなものを使って絶対に水が入らない状態を作らなければなりません。ですのでこの問題の解答は、「理屈の上では浮力ははたらかないが、実験をするとき浮力がはたらかない状態を作るのは大変」ということになります。この問題についてはあれこれ議論が巻き起こりがちなのですが、それはパスカルの原理、水圧の原理、浮力の原理をちゃんと理解していないからです。理解していればシンプルな問題です。物体の下に水分子が潜り込むかどうか、というだけの問題です。潜り込まなければ浮力はまったくはたらかないし、潜り込みさえすれば浮力がはたらきまったく違う状況になる、ということです。

そしてこのとき、底面へ水が何%くらい侵入すると物体が上昇するかという問題もあります。

それは、
物体の形を直方体とし、水面から物体の上面までの深さを \(h\)、物体の高さを \(x\)、物体の密度を \(ρ\) としたときに
　　\({\large\frac{h+ρx}{h+x}}×100\%\)
という式で表されます。

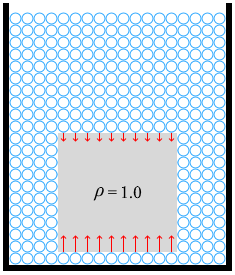\(ρ\) が 1.0 のときは上面までの深さ、物体の高さに関わらず 100% 侵入しなければ浮き上がりません。

左図の水分子に模した球体の1個の重さが 1N だとすると、物体の重さは 1N×100個分 = 100N で、下向きの赤矢印と上向きの赤矢印のベクトル和は上向きに 100N になります。＊物体の重さは2次元で考えて 縦10個分×横10個分=100個分 です。
力関係の様子は2次元で考えても3次元で考えても同じです。
　閉じる

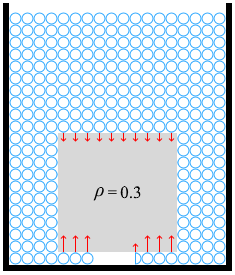深さが 10、高さが 10、密度が 0.3 のときは
　\({\large\frac{h+ρx}{h+x}}×100\%\) = \({\large\frac{10+0.3×10}{10+10}}×100\%\) = \({\large\frac{13}{20}}×100\%\) = 65%
です。

\(ρ\) = 0.3 であれば物体の重さは 100N×0.3 = 30N で、
下向き赤矢印は1本が 10N で、10本あるので 100N、
上向きの赤矢印は1本が 20N で、6.5本あるので 130N です。

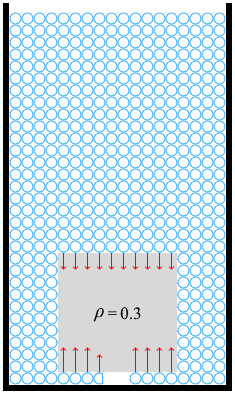深さが 20、高さが 10、密度が 0.3 のときは
　\({\large\frac{h+ρx}{h+x}}×100\%\) = \({\large\frac{20+0.3×10}{20+10}}×100\%\) = \({\large\frac{23}{30}}×100\%\) ≒ 76.7%
です。

物体の重さが 30N で、
下向き赤矢印は1本が 20N で、10本あるので 200N、
上向きの赤矢印は1本が 30N で、7.67本あるので 230N です。

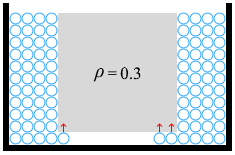深さが 0、高さが 10、密度が 0.3 のときは
　\({\large\frac{h+ρx}{h+x}}×100\%\) = \({\large\frac{0+0.3×10}{0+10}}×100\%\) = \({\large\frac{3}{10}}×100\%\) = 30%
です。