図2のように、長さがそれぞれ l で、質量が 2m と m の細い一様な棒を接合した。このようにして作った棒の両端をA、Bとする。
（問3）棒ABの重心をGとするとき、AGの距離 l1 を式で表わせ。
（問4）図3のように、棒ABの両端に軽い糸をつけ、糸が鉛直に、棒が水平になるように天井につるした。端Aにつけた糸の張力の大きさ TA と、端Bにつけた糸の張力の大きさ TB の比 \(\large{\frac{T_\rm{A}}{T_\rm{B}}}\) を表す式として正しいものを、下の①～⑤のうちから一つ選べ。
① 1 ② \(\large{\frac{l_1}{2l}}\) ③ \(\large{\frac{2l}{\ l_1}}\) ④ \(\large{\frac{l_1}{2l-l_1}}\) ⑤ \(\large{\frac{2l-l_1}{l_1}}\)
#センター14本試
（問3）
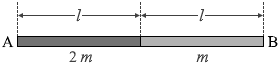
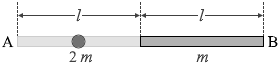質量 2m の一様な棒の重心はその真ん中で、
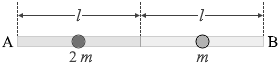質量 m の一様な棒の重心もその真ん中です。
2物体の重心の位置の式（xG = \(\large{\frac{m_1x_1\ +\ m_2x_2}{m_1\ +\ m_2}}\)）を立てますと、
l1 = \(\large{\frac{2m\frac{l}{2}+m\frac{3l}{2}}{2m+m}}\) = \(\large{\frac{2\frac{l}{2}+\frac{3l}{2}}{2+1}}\) = \(\large{\frac{\frac{5l}{2}}{3}}\) = \(\large{\frac{5}{6}}\)l
（暗算で考える場合は）
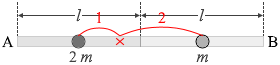重心の位置は質量の逆比、と考えて、\(\large{\frac{5}{6}}\)l と導き出します。
（問4）
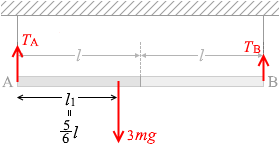重力加速度の大きさを g としますと、棒に掛かる力は
TA 、TB 、3mg の3つです。いま、棒が静止しているということはこれらの力のモーメントの和が 0 になっている（つり合っている）ということだから、（qGACH、qG931参照。右回りを正として）
TA×l1 - TB×(2l - l1) + 3mg×0 = 0
∴ TA×l1 = TB×(2l - l1)
∴ \(\large{\frac{T_\rm{A}}{T_\rm{B}}}\) = \(\large{\frac{2l-l_1}{l_1}}\)
答は ⑤
（ l1 = \(\large{\frac{5}{6}}\)l を代入してみますと）
\(\large{\frac{T_\rm{A}}{T_\rm{B}}}\) = \(\large{\frac{2l-\frac{5}{6}l}{\frac{5}{6}l}}\) = \(\large{\frac{\frac{12}{6}l-\frac{5}{6}l}{\frac{5}{6}l}}\) = \(\large{\frac{12-5}{5}}\) = \(\large{\frac{7}{5}}\)
（暗算で考える場合は）
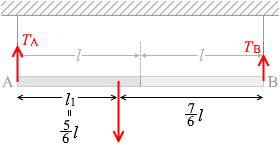力の大きさは重心からの距離の逆比、と考えて \(\large{\frac{T_\rm{A}}{T_\rm{B}}}\) = \(\large{\frac{7}{5}}\) と導き出します。