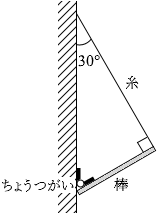
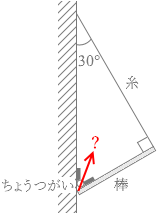
図3のように、質量 m の一様な細い棒の一端を鉛直な壁にちょうつがいでとめ、他端と壁の一点を軽い糸で結んだ。糸と棒は壁に垂直な鉛直面内にあり、壁と糸、棒と糸のなす角度は、それぞれ 30° 、90° であった。糸の張力の大きさ T を式で表わせ。ただし、ちょうつがいはなめらかに回転し、その大きさと質量は無視できるものとする。また、重力加速度の大きさを g とする
#センター15本試物理Ⅰ #センター15本試物理
図3のように、質量 m の一様な細い棒の一端を鉛直な壁にちょうつがいでとめ、他端と壁の一点を軽い糸で結んだ。糸と棒は壁に垂直な鉛直面内にあり、壁と糸、棒と糸のなす角度は、それぞれ 30° 、90° であった。糸の張力の大きさ T を式で表わせ。ただし、ちょうつがいはなめらかに回転し、その大きさと質量は無視できるものとする。また、重力加速度の大きさを g とする
#センター15本試物理Ⅰ #センター15本試物理
棒にはたらく力は、
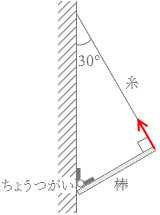張力 T と、
張力は糸に沿った向きにはたらきます。
このようなことはありません。
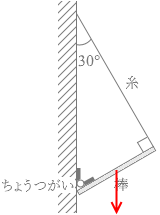重力 mg と、
ちょうつがいからの力の3つです。
ちょうつがいからの力はよく分からないので、この部分を中心として力のモーメントのつり合いの式を立ててみます。
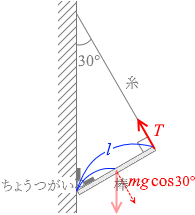（棒の長さを l とし、右回りを正とします）
mgcos30°×\(\large{\frac{l}{2}}\) - T×l = 0
∴ mgcos30°×\(\large{\frac{1}{2}}\) - T = 0
∴ mg\(\large{\frac{\sqrt{3}}{2}}\)×\(\large{\frac{1}{2}}\) - T = 0
∴ T = \(\large{\frac{\sqrt{3}}{4}}\)mg
（余談：3力の作用線は1点で交わる）
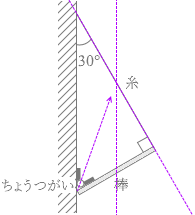3力の作用線は1点で交わるので、ちょうつがいからの力の方向も特定できます。
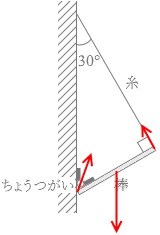上で求めた T の値を考慮して、実際の力の様子を描くと左図のような感じになります。