張力

どこもかしこも同じ大きさ

ひもやロープを引っ張ったときに、引きちぎられないように踏ん張る力を張力といいます。

この張力が各箇所でどのように作用しているのか考えてみます。

ピンと張ったロープを、1万個の微小部分に分割したとします。

左から1番目、2番目、…1万番目とし、一番右側にある1万番の微小部分を右向きに 2.3N の力で引っ張ったとします。

すると1万番は反作用の力として左向きに 2.3N で引っ張り返します。と同時に9999番を右向きに 2.3N で引っ張ります。すると9999番は1万番を左向きに 2.3N で引っ張り、9998番を右向きに 2.3N で引っ張り、…、という風に数珠つなぎとなって 2.3N の力がロープのあらゆる箇所に染み渡ります。

一番左に位置する1番の微小部分は壁を 2.3N で引っ張り、壁から 2.3N で引っ張り返されています。

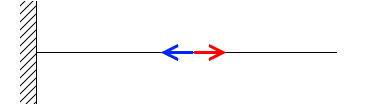たとえば5274番の微小部分は、5275番から右向きに引っ張られ、5273番から左向きに引っ張られ、それらの力がつり合うことによって5274番は静止しています。＊この力関係を数式で表すと、
　　(+2.3) + (-2.3) = 0
となります。

この力によってロープがちぎれた場合は「2.3N の力によってロープがちぎれた」ということになります。「4.6N の力」ではありません。合算してカウントしたりしません。
　閉じる

張力というのは、引っ張った方向の力、引っ張り返す方向の力、両方のことをいいます。そしてこの力はどこもかしこも同じ大きさになっています。

これらのことはチェーンをイメージした方が理解しやすいかもしれません。

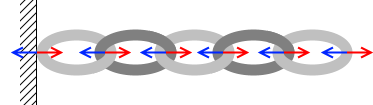どこか一箇所だけ強い力が掛かったとすれば、そこの部分は力がつり合わず、動くことになります。力が拮抗するまでズレ動き、力が拮抗したところで動きが止まります。つまり、いずれ全ての力が同じになるということです。

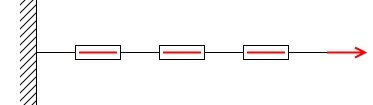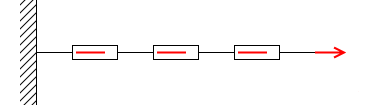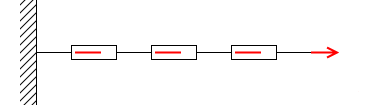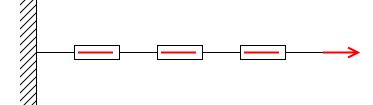実際に目に見える形で確かめるならばバネばかりを用いるといいかもしれません。バネばかりを直列に連結して引っ張ると、その目盛りは全て同じになります。

滑車で曲げられても

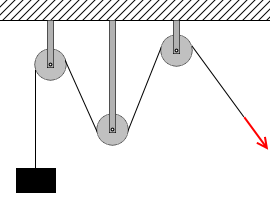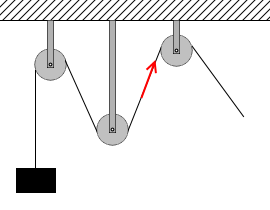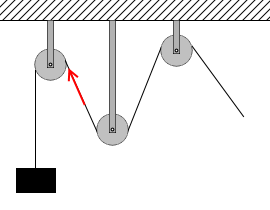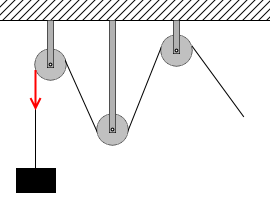二股に別れていたりせず1本でつながっていて、ピンと張っているロープの張力は、滑らかに動く滑車によって曲げられても、どこもかしこも同じ大きさになります＊『糸でつながれた物体』項参照。
　閉じる。ロープ上の張力は同一作用線上にあるといえます。

たとえば靴ひもの張力はどこもかしこも同じ大きさです。

質量が無い

高校物理では、糸、ひも、ロープには質量が無いとする場合が多いです＊『弦の固有振動数』を考えるときは質量を気にします。
　閉じる。あと、伸び縮みしない、としたり、加速中であっても張力はどこもかしこも一定、とする場合が多いです。

たるむと張力 0

当たり前のことですが、張力は引っ張る方向にしかはたらきません。押し込む方向にははたらきません＊ばねの弾性力との大きな違いです。
　閉じる。

そして、糸やロープが少しでもたるんでいるときは張力は 0 です。
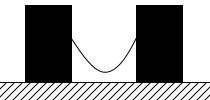左図のような場合、本当は張力は 0 とは言い切れないのですが、高校物理では糸やロープの質量を 0 とする場合が多いので左図のような場合でも張力は 0 とみなします。