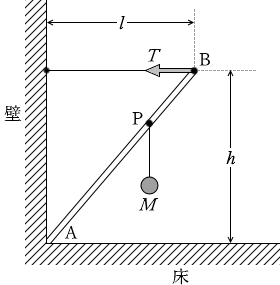
図1のように、質量 M のおもりが軽い糸で点Pからつり下げられた、細くて軽い棒ABが静止している。棒の一端Aは水平な床と鉛直な壁の隅にあり、他端Bは壁につけられた長さ l のひもで引っ張られている。ひもは水平で、床からの高さは h である。棒とひもは同一鉛直面内にあるものとする。 距離APが距離BPの2倍のとき、ひもの張力の大きさ T を式で表わせ。ただし、重力加速度の大きさを g とする。
#センター17本試物理
図1のように、質量 M のおもりが軽い糸で点Pからつり下げられた、細くて軽い棒ABが静止している。棒の一端Aは水平な床と鉛直な壁の隅にあり、他端Bは壁につけられた長さ l のひもで引っ張られている。ひもは水平で、床からの高さは h である。棒とひもは同一鉛直面内にあるものとする。 距離APが距離BPの2倍のとき、ひもの張力の大きさ T を式で表わせ。ただし、重力加速度の大きさを g とする。
#センター17本試物理
棒ABが静止しているということは、棒にはたらく力のモーメントがつり合っているということです。
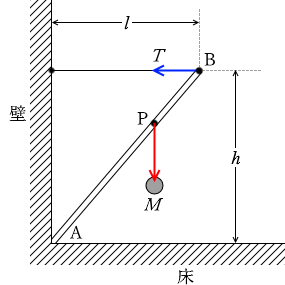A点を中心とした力のモーメントを考えます。
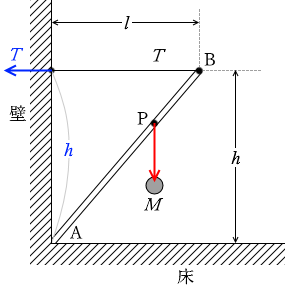張力 T を作用線に沿って移動して考えますと、これによる力のモーメントは
T × h
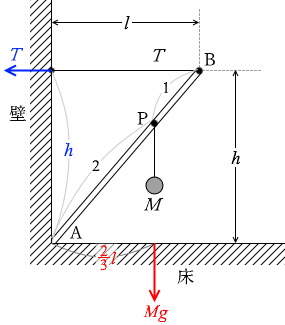同様に、重力 Mg を作用線に沿って移動して考えますと、これによる力のモーメントは
Mg × \(\large{\frac{2}{3}}\)l
この2つの力のモーメントがつり合っているのだから、
T × h = Mg × \(\large{\frac{2}{3}}\)l
∴ T = \(\large{\frac{2l}{3h}}\)Mg
（別解）
『qG931』で説明したように、力のモーメントの大きさを求める考え方は2通りあります。力を作用線に沿って移動するやり方（上記）とそうでないやり方（下記）です。
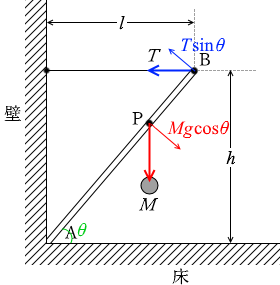棒の仰角を θ と置いて、A点を中心とした力のモーメントを考えます。
張力による力のモーメントは
Tsinθ × \(\large{\frac{h}{\sinθ}}\) = T × h
重力による力のモーメントは
Mgcosθ × \(\large{\frac{2}{3}}\)\(\large{\frac{l}{\cosθ}}\) = Mg × \(\large{\frac{2}{3}}\)l
となり、同じ結果が得られます。しかし、sin と cos はどちらがどちらだか分からなくなりがちなので、無理に θ を設定するやり方は良くないかもしれません。水平方向の長さ、鉛直方向の長さが設定されていて、角度 θ が設定されてないような場合は、力を作用線に沿って移動するやり方を採用してください。