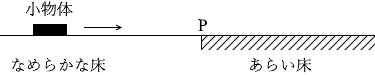
図1のように、水平でなめらかな床の上を等速度ですべってきた小物体が、時刻 t0 で点Pに達し、その後、一様なあらい床の上をすべり続けた。このときの速さ v と時間 t の関係を表すグラフとして最も適当なものを、下の①～⑥のうちから一つ選べ。
#センター02本試
図1のように、水平でなめらかな床の上を等速度ですべってきた小物体が、時刻 t0 で点Pに達し、その後、一様なあらい床の上をすべり続けた。このときの速さ v と時間 t の関係を表すグラフとして最も適当なものを、下の①～⑥のうちから一つ選べ。
#センター02本試
点Pまでの間は等速度なので v-tグラフの曲線は水平になるはずで、①～⑥までそうなっています。
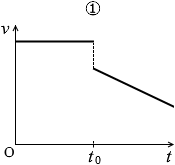
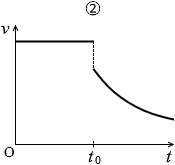
点P以降はあらい床の上をすべるのでスピードが落ちるわけですが、このスピードの落ち方が問題で、この場合には等加速度で落ちていきます。これは摩擦の知識が必要なのですが、物体が動いているときは、どんな力が加わっていてもどんなスピードで動いていても、摩擦力は変わりません。動いているときの摩擦力は物体の重さと接触面の性質だけで決まります（少なくとも高校物理では）。
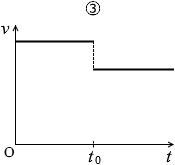
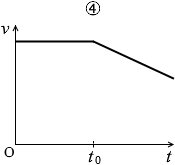
というわけで直線的に速度は減っていくので正しいグラフは①か④です。
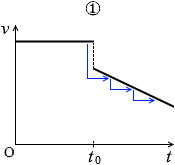①は点Pで突然大幅に減速してますが、これはおかしいです。ハンマーか何かで叩かない限りこうはなりません。
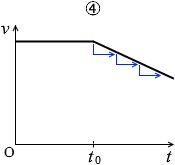点Pにおいても同じ割合で減速していくはずです。
というわけで、最も適当なグラフは ④