摩擦力
常に逆向き
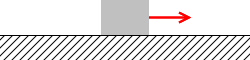床の上に置かれた物体を動かそうとすると、それを邪魔しようとする力が働きます。
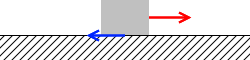その力は物体と物体の間の接触面にはたらきます。この力を摩擦力といいます。物体が動く向きと必ず逆向きです＊
床や台が動かないときはあまり気にしなくていいのですが、
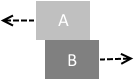摩擦力というものは相対的なものです。
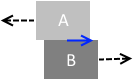物体Bに対して左に動く物体Aにはたらく摩擦力は右向きです。
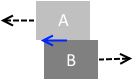物体Aに対して右に動く物体Bにはたらく摩擦力は左向きです。
２つの摩擦力は、大きさが等しく、向きが逆です。作用・反作用の関係にあります。
閉じる。
なお、摩擦力は空気抵抗とは別物です。
接触面の状態による
つるつるの面（たとえばスケートリンク。あるいは潤滑油が塗られた面）の上に置かれた物体は小さな力で動かすことができます。
ざらざらのあらい面（たとえばコンクリート）の上に置かれた物体は大きな力でないと動かすことができません。
押し付ける力による
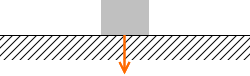床面に押し付ける力が強いほど摩擦力は強くなります。
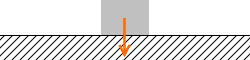水平の床に置かれている場合は、押し付ける力というのは、物体に掛かる重力と同じ大きさです。上から手で押さえ付けたりすれば、さらに大きくなります。
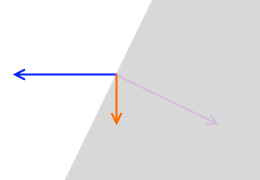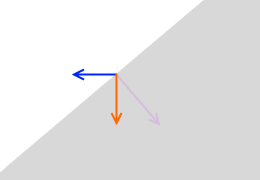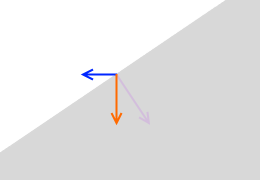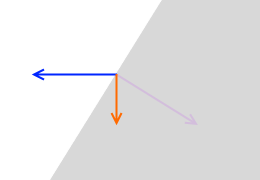
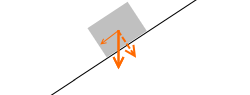斜面の上では押し付ける力は小さくなります。
押し付ける力の向きというのは接触面に垂直です。
摩擦力の式
摩擦力の大きさは、接触面の状態と押し付ける力の２つの要素で決まります。
接触面の状態がどれだけ摩擦力に影響を及ぼすかという指標が摩擦係数です。μ ＊ギリシア文字の「ミュー」です。語源はわかりません。閉じるで表します。静止摩擦係数と動摩擦係数があります。物体の素材等で決まります。鋼鉄と鋼鉄との静止摩擦係数が 0.8 くらい＊鋼鉄製の台の上に置いた鋼鉄製の（10Nの重力が掛かる）物体を動かすには 8N くらいの力が必要。
閉じるで、動摩擦係数はもうちょっと小さく、潤滑油を塗った場合はさらに大幅に小さくなります。金属同士の摩擦係数は大抵 0.3~0.9 くらいです＊下で説明しますが、摩擦係数はちょっとした条件の変化で大きく変わるので、この金属とあの金属をこすり合わせるときの数値はコレ、とはハッキリいえません。製品を製造するときなどは実験を繰り返して詳しく調べる必要があります。
また、数値が 1.0 を超えるというようなことは聞いたことがないのですが、理論上は 1.0 を超えることもあり得ます。（ちなみに、1.0 を超えるときというのは『摩擦角』が 45° を超えます。）
たとえば、境界面の形がこんなだったりしたら、摩擦係数は数百、数千という値になります。しかしこのような場合を『摩擦』と定義するのかは微妙です。
摩擦係数の値が負になることはありません。
閉じる。
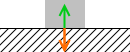押し付ける力については、高校物理では、その替わりに垂直抗力を用います。N ＊normal（垂直の）から。閉じるで表します。押し付ける力と垂直抗力は、作用・反作用の関係にあり、大きさが同じで向きが逆です。実質的に同じものです。＊なぜ高校物理で『垂直抗力』を用いるのかはわかりません。『押し付ける力』ではフレーズが長すぎるからかもしれないし、床にはたらく力でなく物体にはたらく力に着目すべきという考えなのかもしれませんし、垂直抗力とは別の『抗力』のことを意識させたいのかもしれません。
大学物理では『荷重』とか『垂直荷重』という言葉が使われることが多いです。閉じる
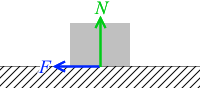摩擦力を F ＊frictional force（摩擦による力）もしくは、ただ単に force（力）から。閉じるとしますと、μ と N を用いて、以下のように表せます。
摩擦力
F = μN
摩擦力と垂直抗力と抗力
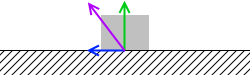摩擦力と垂直抗力を足したものを抗力といいます。
なめらかな面・あらい面
高校物理では、摩擦の無い接触面をなめらかな面、摩擦のある接触面をあらい面と呼ぶことになっています。お約束です。問題文に「なめらかな面」と出てきたらそれは摩擦力を 0 とみなしなさいという意味です。
摩擦力は、物体の下面の微小な山切り型の凸凹と、床面の微小な山切り型の凸凹が引っ掛かることによって生じると考えられます。
凸凹がするどく突き出ているほど、山を乗り越えるのが大変になり、摩擦力が大きくなります。
物体が重くなるほど、山を乗り越えるのが大変になり、摩擦力が大きくなります。
接触面を拡大しますと、このようになっていますが、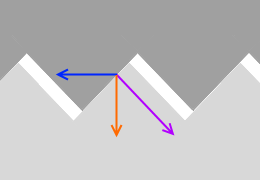
山切りの角度が急になるということは摩擦係数 μ が大きくなって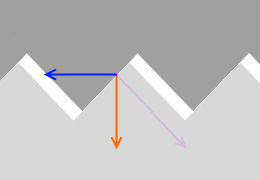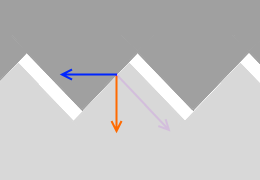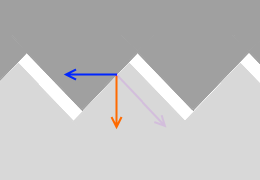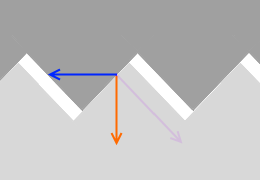
それによりますと、
だいたい、山と山の間隔が合うなんてことは無いし、
境界面の形は非常に複雑で、大小の山が複雑に組み合わされていて、実際にはミクロな山と山のこすれ合いになっているはずで、いったいどの山とどの山のこすれ合いを評価すればいいのかわからないですし、