qHAEB

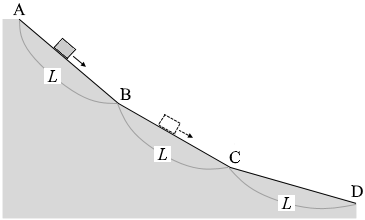
（問1）
動摩擦力というものは物体のスピードが変化しても一定です。また、物体に掛かる重力の大きさも一定です（重力の運動方向の成分は斜面の角度によって変化します）。つまり小物体は各区間で等加速度直線運動をします。

等加速度直線運動の公式として

　　v = v₀ + at

　　x = v₀t + \(\frac{1}{2}\)at²

　　v² - v₀² = 2ax

という3つの式がありますが、一番目の式に各量（点Aでの速さは 0、点Bでの速さは v₁、その間の時間は t₁）を代入すると、

　　　　v₁ = 0 + αt₁　　……➊

三番目の式に各量を代入すると、

　　　　v₁² - 0² = 2αL　　➊式を代入して

　∴　　(αt₁)² - 0² = 2αL

　∴　　(αt₁)² = 2αL

　∴　　αt₁² = 2L　　……➋

　∴　　t₁² = \(\large{\frac{2L}{α}}\)

　∴　　 t₁ = \(\sqrt{\large{\frac{2L}{α}}}\) 　　……❸

答えは ⑥ です。

（問2）
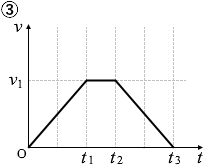
AB間とCD間の距離は同じであるので、AB間での加速の度合いとCD間での減速の度合いは同じであり、運動している時間も同じです。そうでなければスタート時とゴール時で同じスピード（速さ 0 ）にはなり得ません。よって、②、④、⑥は不適です。

そして、AB間、CD間でのスピードは遅かったり速かったりしますが、BC間ではずっと速いままです。つまりBC間の運動時間は短いはずです。

というわけで答えは ③ です。

（式を使って考える）
点Cから点Dまで進むのに掛かる時間 (t₃ - t₂) を T₃ 、その間の小物体の加速度を α₃ (α₃ < 0) と置きます。

問1で示した等加速度直線運動の公式の一番目の式に各量を代入すると、

　　　　0 = v₁ + α₃T₃　　……❹

公式の三番目の式に各量を代入すると、

　　　　0² - v₁² = 2α₃L　　❹式を代入して

　∴　　0² - (- α₃T₃)² = 2α₃L

　∴　　(- α₃T₃)² = - 2α₃L

　∴　　α₃²T₃² = - 2α₃L

　∴　　T₃² = - \(\large{\frac{2L}{α_3}}\)

　∴　　T₃ = \(\sqrt{- \large{\frac{2L}{α_3}}}\)　　……❺

また、➊式を❹式に代入すると、

　　　　0 = αt₁ + α₃T₃

これに❸式、❺式を代入すると、

　　　　0 = α\(\sqrt{\large{\frac{2L}{α}}}\) + α₃\(\sqrt{- \large{\frac{2L}{α_3}}}\)

　∴　　0 = α\(\sqrt{\large{\frac{1}{α}}}\) + α₃\(\sqrt{- \large{\frac{1}{α_3}}}\)

　∴　　- α₃\(\sqrt{- \large{\frac{1}{α_3}}}\) = α\(\sqrt{\large{\frac{1}{α}}}\)　　両辺2乗して

　∴　　α₃²⋅(\(- \large{\frac{1}{α_3}}\)) = α²⋅(\(\large{\frac{1}{α}}\))

　∴　　- α₃ = α

　∴　　α₃ = - α　　……(ⅰ)

これを❺式に代入して、

　　　　T₃ = \(\sqrt{\large{\frac{2L}{α}}}\)

つまり、

　　　　T₃ = t₁　　……(ⅱ)

そして、点Bから点Cまで掛かる時間 (t₂ - t₁) を T₂ と置いて、問1で示した等加速度直線運動の公式の二番目の式に各量を代入すると、

　　　　L = v₁T₂ + \(\large{\frac{1}{2}}\)⋅0⋅T₂

　∴　　L = v₁T₂

この式と➊式を➋式に代入すると、

　　　　αt₁² = 2L

　∴　　\(\large{\frac{v_1}{t_1}}\)t₁² = 2v₁T₂

　∴　　t₁ = 2T₂　　……(ⅲ)

(ⅰ)式より、AB間での加速の度合いとCD間での減速の度合いが同じであることが分かり、
(ⅱ)式より、AB間とCD間で掛かる時間が同じであることが分かり、
(ⅲ)式より、AB間、CD間に掛かる時間よりBC間に掛かる時間の方が短いことが分かります。

（余談：グラフの面積）
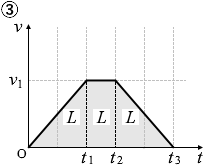t軸と曲線で囲まれる面積は小物体の移動距離を表わします。総計で 3L です。