等加速度直線運動

直線上

加速度が一定の運動を等加速度運動といいます。
このうち、直線上の運動である場合を等加速度直線運動といいます。＊等加速度運動と等加速度直線運動は完全にはイコールではありません。
等加速度運動ではあるけれども直線上ではないパターンがあります。水平投射や斜方投射です。
（等速円運動の加速度は、大きさについては一定ですが向きについては変化していますので等加速度運動ではありません。ややこしいです。）

速度に関しては、
等速直線運動と等速度運動と等速度直線運動は完全にイコールです。
３番目の等速度直線運動という言葉は使われることはほとんどありません。１番目の等速直線運動という言葉がもっとも多く使われます。
　閉じる
本項では、等加速度直線運動を表す３つの有名な公式について説明します。

等加速度直線運動の速度

直線上を一定の加速度 a [m/s²] で進む物体の運動を考えます。

時刻 t=0 [s] のときの速度（=初速度）を v₀ [m/s] とすると、加速度 a [m/s²] というのは1秒当たり a [m/s] ずつ速度が増すという意味だから、t [s] 後の速度 v [m/s] は、

　　　　v = v₀ + a t　　……①

この式は『平均の加速度』の式

　　　　\(\bar{a}\) = \(\large{\frac{v_2-v_1}{t_2-t_1}}\)

を変形することによっても導き出せます。ここでは　\(\bar{a}\) ⇒ a、v₂ ⇒ v、v₁ ⇒ v₀、t₂-t₁ ⇒ t　だから、

　　　　a = \(\large{\frac{v-v_0}{t}}\)

　∴　　a t = v - v₀

　∴　　v = v₀ + a t

等加速度直線運動の変位

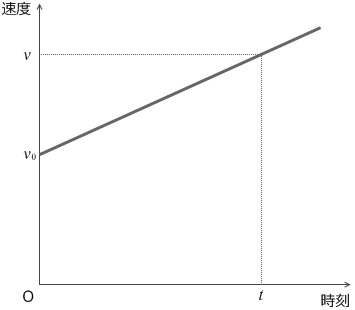上で示した運動を v-tグラフにすると左図のようになります。

『変位と速度と加速度』の『微分・積分』で、v-tグラフにおいて曲線とt軸で挟まれる部分の面積を求めることによって変位を導き出せることを説明しました。その面積を求めて、変位 x [m] を導き出してみますと、

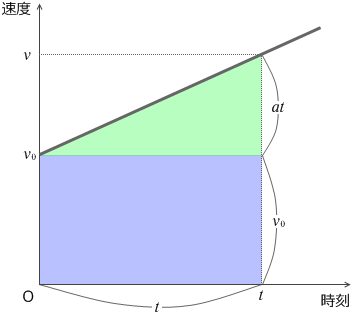　　x = +

　　　= v₀ t + \(\frac{1}{2}\)at²　　……②

あるいは、台形の面積の公式を使って導き出すことができます。

　　x = (上底+下底) × 高さ × \(\frac{1}{2}\)

　　　= (v₀ + v₀ + a t) × t × \(\frac{1}{2}\)

　　　= v₀ t + \(\frac{1}{2}\)at²

時間 t を含まない式

①式を変形して②式に代入すると、時間 t を含まない式が得られます。

　① →　　v = v₀ + a t　⇒　t = \(\large{\frac{v-v_0}{a}}\)

　② →　　x = v₀ t + \(\frac{1}{2}\)at²

　　　　　　= v₀ \(\bigl(\large{\frac{v-v_0}{a}}\bigr)\) + \(\frac{1}{2}\) a \(\bigl(\large{\frac{v-v_0}{a}}\bigr)^2\)

　　　　　　= \(\large{\frac{v_0}{a}}\) (v - v₀) + \(\frac{1}{2a}\) (v - v₀)²

　　　　　　= \(\large{\frac{v_0}{a}}\) (v - v₀) + \(\frac{1}{2a}\) (v² - 2 v v₀ + v₀²)

　∴　　2ax = 2 v₀ (v - v₀) + (v² - 2 v v₀ + v₀²)

　　　　　　= 2 v v₀ - 2 v₀² + v² - 2v v₀ + v₀²

　　　　　　= v² - v₀²　　……③

この式は、等加速度直線運動の問題で時間 t が与えられていない場合に使います。

まとめ

①式、②式、③式をまとめます。

この式を扱うときは正負に注意してください。

加速度が負の場合

上式は加速度が負の場合でも成り立ちます。

加速度が負のときは x-tグラフ、v-tグラフ、a-tグラフの様子が『変位と速度と加速度』で示したものとはだいぶ違ってきます。

x-tグラフは②式で表されますが、この式は数学でいうところの2次関数なので、グラフは放物線であるのですが、2次の項の係数である a（加速度）が -（マイナス）でありますと、グラフは上に凸の放物線となります。

いま、初速度 v₀>0、加速度 a<0 であるとします。真上に投げ上げたボールが重力によって再び落下してくるような運動です。

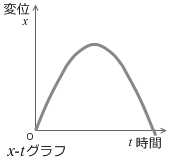始めは初速によって＋の方向に向かいますが、やがて止まり、そして逆向きに進んでいきます。x-tグラフは上に凸の放物線になります。

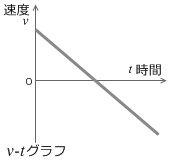速度に関しては、単位時間あたり a ずつ一定の割合で減っていき、やがて 0 になり、そして - になります。この v-tグラフは上の x-tグラフの傾き（=速度）の変化を表しています。

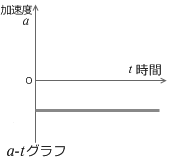加速度は一定なのだから a-tグラフは一定です。加速度 a は負のままです。このグラフは上の v-tグラフの傾き（=加速度）の変化を表しています。