図2のように、質量 M の物体Aと質量 m の物体Bを糸でつないであらい水平面上に置き、Aを水平右向きの力で引いて、AとBをともに一定の速さ v で運動させた。このとき、力の大きさは F であった。水平面とA、Bの間の動摩擦係数をそれぞれ μ'A 、μ'B とする。また、重力加速度の大きさを g とする。
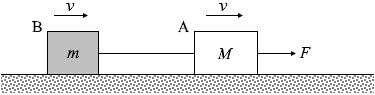
（問3）F を式で表せ。
（問4）Aに力を加えるのをやめたところ、糸がゆるみ、AとBは図3のように糸がゆるんだまましばらく運動を続け、やがて互いに衝突することなく静止した。力を加えるのをやめてからA、Bがそれぞれ静止するまでにかかった時間を tA 、tB とする。μ'A と μ'B 、および、tAと tB の大小関係の組合せとして正しいものを、下の①～⑥のうちから一つ選べ。
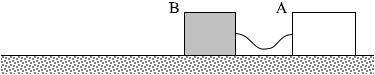
① μ'A > μ'B 、tA > tB ② μ'A < μ'B 、tA > tB ③ μ'A > μ'B 、tA = tB ④ μ'A < μ'B 、tA = tB ⑤ μ'A > μ'B 、tA < tB ⑥ μ'A < μ'B 、tA < tB
#センター11本試
（問3）
一定の速さで運動しているということは、複数ある力の合力は 0 であるということです。
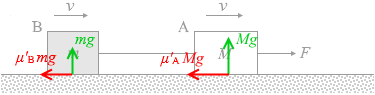物体Aにはたらく動摩擦力は μ'AMg で、
物体Bにはたらく動摩擦力は μ'Bmg で、
これらの力と F はつり合っているので、
F = (μ'AM + μ'Bm)g
（問4）
力を加えるのをやめた後の物体Aの加速度を aA として、物体Aの運動方程式（ma = F）を立てますと、
MaA = μ'AMg
∴ aA = μ'Ag
同じように、物体Bの加速度を aB として、物体Bの運動方程式を立てますと、
maB = μ'Bmg
∴ aB = μ'Bg
糸がゆるんだということは物体Aの方が減速幅が大きいということだから、
μ'Ag > μ'Bg
∴ μ'A > μ'B ……①
そして、
始め、v で動いていた物体Aが、μ'Ag で徐々に減速していき
高校物理においては、物体の速さが変わっても動摩擦力は変わらないことになっています。
動摩擦力が変わらないので加速度も変わりません。物体の運動は等加速度運動です。
、tA だけ経ったときに速さが 0 になるということだから、
v - μ'AgtA = 0
∴ tA = \(\large{\frac{v}{μ{_\rm{A}}'g}}\)
同様に、物体Bの速さも、
v - μ'BgtB = 0
∴ tB = \(\large{\frac{v}{μ{_\rm{B}}'g}}\)
①の関係より、
\(\large{\frac{v}{μ{_\rm{A}}'g}}\) < \(\large{\frac{v}{μ{_\rm{B}}'g}}\)
∴ tA < tB
答えは ⑤
（本問を見たときに、物体が衝突しない条件を求める問題なのかと一瞬思いますが、糸の長さが提示されてないのでその条件は求められません。単に μ'A 、μ'B 、tA 、tB の大小関係を求める問題です。）