ばね定数の異なる軽いばねAとBがある。図2のように、それぞれのばねの一端を天井に取り付け、もう一方の端に質量 \(m\) のおもりを取り付けた。すると、ばねAは自然の長さから \(a\) だけ伸びたところで、ばねBは自然の長さから \(2a\) だけ伸びたところで、それぞれつりあいの状態になっておもりが静止した。
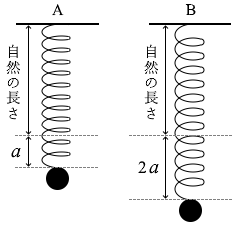
このとき、ばねBの弾性力による位置エネルギーは、ばねAの弾性力による位置エネルギーの何倍か。
#共テ23本試物理基礎
ばね定数の異なる軽いばねAとBがある。図2のように、それぞれのばねの一端を天井に取り付け、もう一方の端に質量 \(m\) のおもりを取り付けた。すると、ばねAは自然の長さから \(a\) だけ伸びたところで、ばねBは自然の長さから \(2a\) だけ伸びたところで、それぞれつりあいの状態になっておもりが静止した。
このとき、ばねBの弾性力による位置エネルギーは、ばねAの弾性力による位置エネルギーの何倍か。
#共テ23本試物理基礎
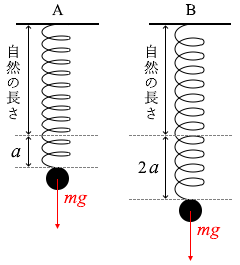まず、ばね定数について考えてみます。
双方に同じ力が掛かっていて、ばねAの伸びは半分、なのだからばねAのばね定数はばねBの倍です。ばねAのばね定数を \(k_\rm{A}\) 、ばねBのばね定数を \(k_\rm{B}\) と置きますと、フックの法則より
\(mg = k_{\rm{A}}a\)
\(mg = k_{\rm{B}}・2a\)
∴ \(k_{\rm{A}} =2k_\rm{B}\)
次に、弾性力による位置エネルギーについて考えてみます。
それぞれ \(U_\rm{A}\)、\(U_\rm{B}\) と置きますと、
\(U_{\rm{A}}\ = \frac{1}{2}k_{\rm{A}}a^2\)
\(U_{\rm{B}}\ = \frac{1}{2}k_{\rm{B}}(2a)^2\)
∴ \({\large\frac{U_{\rm{B}}}{U_{\rm{A}}}} = {\large\frac{\frac{1}{2}k_{\rm{B}}(2a)^2}{\frac{1}{2}k_{\rm{A}}a^2}} = {\large\frac{k_{\rm{B}}・4}{k_{\rm{A}}}} = {\large\frac{k_\rm{B}・4}{2k_{\rm{B}}}} = 2\)
というわけで、ばねBの弾性力による位置エネルギーは、ばねAの弾性力による位置エネルギーの 2倍 です。
これは、同じ力を加えたとき、柔らかいばねの方が弾性エネルギーが大きいということです。
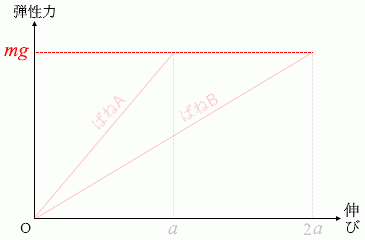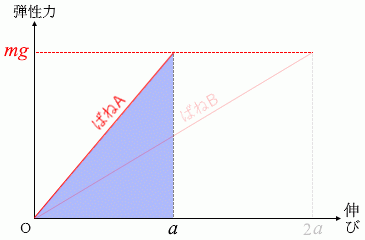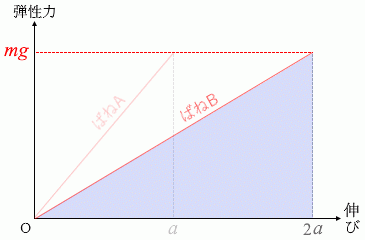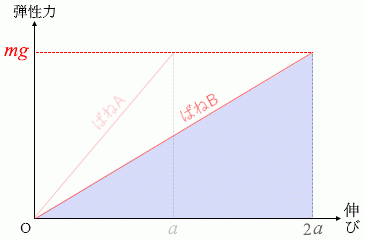縦軸を弾性力、横軸をばねの伸びとした左図のようなグラフでは青色の三角形の部分が弾性エネルギーとなるわけですが、この三角形の面積は底辺の長さに比例します。底辺の長さはばね定数に反比例します。