弾性力
反作用の力
ばねを伸ばそうとすると、縮めようとする力がはたらきます。縮めようとすると伸ばそうとする力がはたらきます。このような元に戻ろうとする力を弾性力といいます。作用⋅反作用の法則にのっとった反作用の力です。
復元力という言葉もあります。ほぼ同じ意味です。*それぞれの言葉の厳密な定義はちょっと分からないのですが、
・分子間力に基づく力の場合は弾性力、復元力、どちらも用いられ
・万有引力に基づく力の場合は復元力のみを用いる
ような気がします。
ばねの力の大本は分子間力です。分子間力の大本は電磁気力です。
閉じる
弾性力がはたらかない物質
粘土でできた物体は押し込んだら押し込まれたままで、引っ張られたら引っ張られたままです。元の形に戻りません。このような物質には弾性力ははたらきません。ばねやロープも、引きちぎれてしまったら弾性力ははたらきません。
フックの法則
フックの法則
ばねの弾性力には大きな特徴があり、それは、力の大きさが目に見えるということです。ばねの伸び、あるいは縮みとして目に見える形で現れます。物理では珍しいことです。
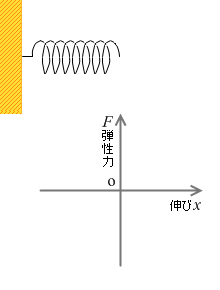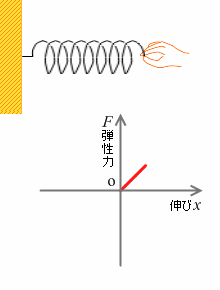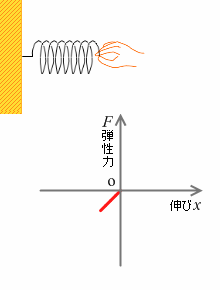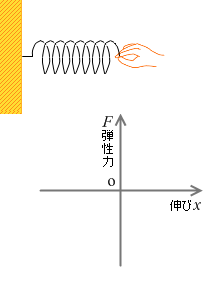 伸び縮みの長さは弾性力の大きさにきれいに比例します。(といいますか、高校物理ではそのようなばねについて考えます)。ばね秤は、ばねの伸びの長さによって物の重さを表示する装置です。
伸び縮みの長さは弾性力の大きさにきれいに比例します。(といいますか、高校物理ではそのようなばねについて考えます)。ばね秤は、ばねの伸びの長さによって物の重さを表示する装置です。
ばねの伸び縮みの長さを x [m] 、弾性力の大きさを F [N] とすると、
F = k x
という関係があります。フックの法則といいます*17世紀にイギリスのロバート・フックという物理学者が発見しました。
閉じる。
k はばね定数と呼ばれる比例定数です*ドイツ語 Konstant の頭文字。単位は [N/m] ニュートン毎メートル です。
k という文字はフックの法則以外にも様々な法則で使われる量記号です。
閉じる。ばねの伸びにくさを表します。グラフの傾きです。k が大きいと、伸ばすのに、大きい F が必要になります。
しかし、上式では厳密には不正確です。正負を厳密に考える、すなわちベクトルとして厳密に考えると間違いです。
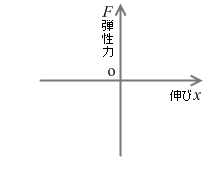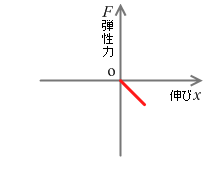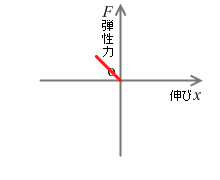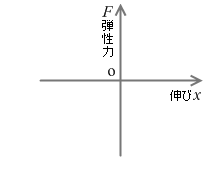 右向きを正とすると、変位 x が正のとき、弾性力 F の向きは左向き、すなわち負なのです。変位 x が負のときは、弾性力 F の向きは正です。ですので厳密なフックの法則の式は以下のようになります。グラフについては左図のようになります。
右向きを正とすると、変位 x が正のとき、弾性力 F の向きは左向き、すなわち負なのです。変位 x が負のときは、弾性力 F の向きは正です。ですので厳密なフックの法則の式は以下のようになります。グラフについては左図のようになります。
*
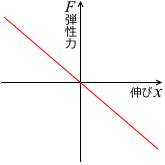 ばねの弾性力は、伸ばすときも押しこむときも大きさは同じです。ばね定数(グラフの曲線の傾き)は一定です。
ばねの弾性力は、伸ばすときも押しこむときも大きさは同じです。ばね定数(グラフの曲線の傾き)は一定です。
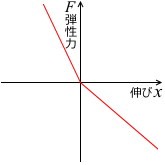 伸ばすときよりも、押しこむときの方が固い、などというようなばねはあまり存在しません。
伸ばすときよりも、押しこむときの方が固い、などというようなばねはあまり存在しません。
 たいていのばねは金属でできていて、
たいていのばねは金属でできていて、
 各部分が曲がることによって、ばねが伸び縮みするわけですが、
各部分が曲がることによって、ばねが伸び縮みするわけですが、
 右に曲がるときと左に曲がるときで曲がり方が違うという金属はあまりありません。ですので、ばね全体として、伸び方と縮み方は同じ、ということになります。
右に曲がるときと左に曲がるときで曲がり方が違うという金属はあまりありません。ですので、ばね全体として、伸び方と縮み方は同じ、ということになります。
閉じる
(弾性エネルギーについては『弾性力による位置エネルギー』項をご覧ください。)
ばねの直列接続
ばねを直列につなげると伸ばしやすくなるでしょうか伸ばしにくくなるでしょうか。
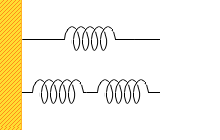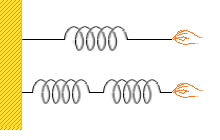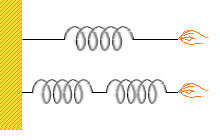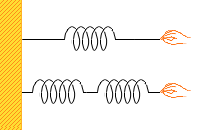 同じばねを3つ用意して、ばねが1つだけの場合と、ばねを2つ直列につなげた場合とで比較してみます。どちらも20cm伸ばすとすると、フックの法則から、1つの場合の弾性力は F₁=0.2×k [N] 。2つの場合は各10cmだけ伸びることになるから1つ当たりの弾性力は F₂=0.1×k [N] 。
同じばねを3つ用意して、ばねが1つだけの場合と、ばねを2つ直列につなげた場合とで比較してみます。どちらも20cm伸ばすとすると、フックの法則から、1つの場合の弾性力は F₁=0.2×k [N] 。2つの場合は各10cmだけ伸びることになるから1つ当たりの弾性力は F₂=0.1×k [N] 。
そうしますと、2つつなげた場合の弾性力は2倍の 2×F₂=0.2×k [N] でしょうか?
違います。
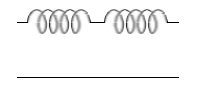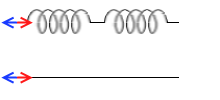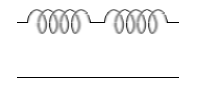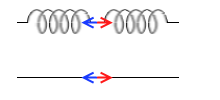 直列接続のばねを伸ばしたときには各部分にまったく同じ力がはたらいています。途中が F₂[N] ならどこもかしこも F₂[N] です。ばねを伸ばして静止した状態というのは力がつり合った状態です。ばねの各微小部分同士が同じ力で引っ張り合ってるので静止しているのです。ミクロな視点でいえば、ばねを構成する原子たちがお互いを F₂[N] で引っ張り合ってつり合って静止しているのです。同じ力ではないということは力のバランスがくずれて物体が動くということになってしまいます。ばねが振動してしまっているときなどがそうです。
直列接続のばねを伸ばしたときには各部分にまったく同じ力がはたらいています。途中が F₂[N] ならどこもかしこも F₂[N] です。ばねを伸ばして静止した状態というのは力がつり合った状態です。ばねの各微小部分同士が同じ力で引っ張り合ってるので静止しているのです。ミクロな視点でいえば、ばねを構成する原子たちがお互いを F₂[N] で引っ張り合ってつり合って静止しているのです。同じ力ではないということは力のバランスがくずれて物体が動くということになってしまいます。ばねが振動してしまっているときなどがそうです。
ばね以外でも、たとえばピンと張って静止した1本の糸でも同様のことがいえます。端っこでも途中でもどの部分においても各微小部分同士は同じ力で引っ張り合ってつり合って静止しています。
というわけで2つつなげた場合の弾性力は 2×F₂[N] ではなくて F₂=0.1×k [N] です。ばねが1つのときの F₁=0.2×k [N] の半分です。2つつなげた方が伸ばす力がいらない、すなわち伸ばしやすくなるのです。このことは、ばねというものは、同じ材質、同じ形状なら長い方が伸ばしやすい、つまりばね定数が小さいということを意味します。
ではさらに、ばね定数が違うばねをつなげた場合はどうなるでしょうか。
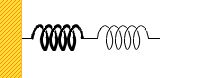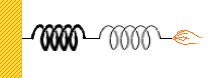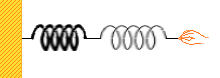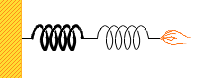 それぞれのばね定数を k₁ 、k₂ 、伸びを x₁ 、x₂ とし、力 F で引っ張るとします。
それぞれのばね定数を k₁ 、k₂ 、伸びを x₁ 、x₂ とし、力 F で引っ張るとします。
それぞれのばねにかかる力は上で説明したように F だから、それぞれのばねでのフックの法則の式は、
F = k₁x₁ 、F = k₂x₂
変形すると以下のようになります。
x₁ = \(\large{\frac{F}{\ k_1}}\) 、x₂ = \(\large{\frac{F}{\ k_2}}\)
2つ合わせて1つのばねとみなしたときのばね定数を K(大文字)として、フックの法則の式を考えてみると、このときの伸びは (x₁+x₂) だから、
F = K(x₁+x₂) 代入して
= K(\(\large{\frac{F}{\ k_1}}\)+\(\large{\frac{F}{\ k_2}}\)) 両辺を F で割って
∴ 1 = K(\(\large{\frac{1}{\ k_1}}\)+\(\large{\frac{1}{\ k_2}}\))
∴ \(\large{\frac{1}{K}}\) = \(\large{\frac{1}{\ k_1}}\)+\(\large{\frac{1}{\ k_2}}\)
となり、この式を満たす K が合成されたばねのばね定数となります。
ばねを直列にたくさん付け加えていくと、K が小さくなっていきます。伸びやすくなります。
この式は電気抵抗の並列接続の式、あるいはコンデンサーの直列接続の合成容量の式とそっくりです。
ばねの並列接続
ばねを並列につなげた場合はどうでしょうか。
 重い荷物を持つ場合は2人で持てば半分の力で済みます。
重い荷物を持つ場合は2人で持てば半分の力で済みます。
 2人対1人で綱引きをすれば2人の方が勝ちます。
2人対1人で綱引きをすれば2人の方が勝ちます。
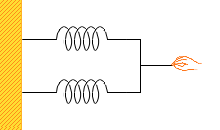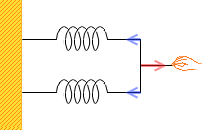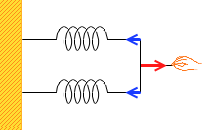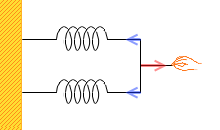 つまり同じばねを2つ並列につなげると、1つのときに比べて倍の力が必要です。ばねは伸びにくくなるのです。2つで1つのばねと見なしたときのばね定数は2倍になります。
つまり同じばねを2つ並列につなげると、1つのときに比べて倍の力が必要です。ばねは伸びにくくなるのです。2つで1つのばねと見なしたときのばね定数は2倍になります。
では、ばね定数が違う2つのばねを並列につなげた場合はどうなるでしょうか。
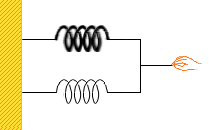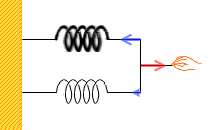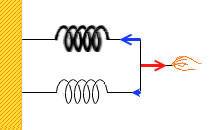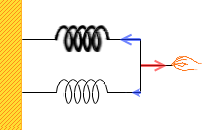 (左図のような装置では実際に引っ張った際には硬いばねの方にワイヤーが片寄ってしまいますが、ここでは理論上、片寄らないで両方とも同じ長さだけ伸ばされることとします。)
(左図のような装置では実際に引っ張った際には硬いばねの方にワイヤーが片寄ってしまいますが、ここでは理論上、片寄らないで両方とも同じ長さだけ伸ばされることとします。)
それぞれのばね定数を k₁ 、k₂ とし、力 F で引っ張り、 x だけ伸びたとします。このときそれぞれのばねに加わる力を F₁ 、F₂ とします。
それぞれのばねでのフックの法則の式は、
F₁ = k₁x 、F₂ = k₂x (上の直列のときは F = k₁x₁ 、F = k₂x₂ でした。*直列のときは F が共通で、並列のときは x が共通です。
閉じる)
2つ合わせて1つのばねと見なしたときのばね定数を K とするとフックの法則の式は、
F = K x (F = F₁ + F₂ だから)
∴ F₁ + F₂ = K x
∴ k₁x + k₂x = K x
∴ k₁ + k₂ = K
となり、この式を満たす K が合成されたばねのばね定数となります。
並列の場合は単純に足すだけです。ばねは伸びにくくなります。これはばねが太くなったことにたとえられます。ばねは太い方が伸びにくいです。
まとめて例示
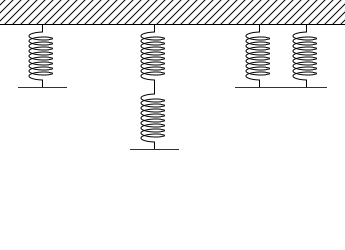
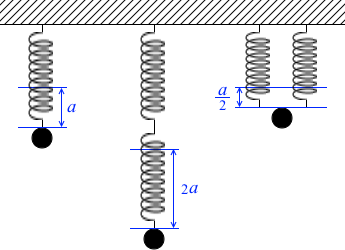
同じばね定数のばね(質量無し)を5個、同じ質量のおもりを3個、用意して以下のように吊り下げると、
伸びはそれぞれ、 a 、2a 、\(\color{#00f}{\large{\frac{a}{2}}}\)
ばね定数はそれぞれ、k 、\(\color{#f00}{\large{\frac{k}{2}}}\) 、2k
となります。
 伸び縮みの長さは弾性力の大きさにきれいに比例します。(といいますか、高校物理ではそのようなばねについて考えます)。ばね秤は、ばねの伸びの長さによって物の重さを表示する装置です。
伸び縮みの長さは弾性力の大きさにきれいに比例します。(といいますか、高校物理ではそのようなばねについて考えます)。ばね秤は、ばねの伸びの長さによって物の重さを表示する装置です。 右向きを正とすると、変位 x が正のとき、弾性力 F の向きは左向き、すなわち負なのです。変位 x が負のときは、弾性力 F の向きは正です。ですので厳密なフックの法則の式は以下のようになります。グラフについては左図のようになります。
右向きを正とすると、変位 x が正のとき、弾性力 F の向きは左向き、すなわち負なのです。変位 x が負のときは、弾性力 F の向きは正です。ですので厳密なフックの法則の式は以下のようになります。グラフについては左図のようになります。 ばねの弾性力は、伸ばすときも押しこむときも大きさは同じです。ばね定数(グラフの曲線の傾き)は一定です。
ばねの弾性力は、伸ばすときも押しこむときも大きさは同じです。ばね定数(グラフの曲線の傾き)は一定です。 伸ばすときよりも、押しこむときの方が固い、などというようなばねはあまり存在しません。
伸ばすときよりも、押しこむときの方が固い、などというようなばねはあまり存在しません。 たいていのばねは金属でできていて、
たいていのばねは金属でできていて、 各部分が曲がることによって、ばねが伸び縮みするわけですが、
各部分が曲がることによって、ばねが伸び縮みするわけですが、 右に曲がるときと左に曲がるときで曲がり方が違うという金属はあまりありません。ですので、ばね全体として、伸び方と縮み方は同じ、ということになります。
右に曲がるときと左に曲がるときで曲がり方が違うという金属はあまりありません。ですので、ばね全体として、伸び方と縮み方は同じ、ということになります。
 同じばねを3つ用意して、ばねが1つだけの場合と、ばねを2つ直列につなげた場合とで比較してみます。どちらも20cm伸ばすとすると、フックの法則から、1つの場合の弾性力は F₁=0.2×k [N] 。2つの場合は各10cmだけ伸びることになるから1つ当たりの弾性力は F₂=0.1×k [N] 。
同じばねを3つ用意して、ばねが1つだけの場合と、ばねを2つ直列につなげた場合とで比較してみます。どちらも20cm伸ばすとすると、フックの法則から、1つの場合の弾性力は F₁=0.2×k [N] 。2つの場合は各10cmだけ伸びることになるから1つ当たりの弾性力は F₂=0.1×k [N] 。 直列接続のばねを伸ばしたときには各部分にまったく同じ力がはたらいています。途中が F₂[N] ならどこもかしこも F₂[N] です。ばねを伸ばして静止した状態というのは
直列接続のばねを伸ばしたときには各部分にまったく同じ力がはたらいています。途中が F₂[N] ならどこもかしこも F₂[N] です。ばねを伸ばして静止した状態というのは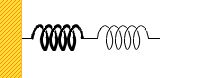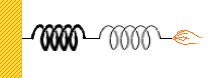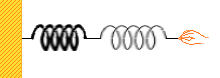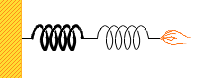 それぞれのばね定数を k₁ 、k₂ 、伸びを x₁ 、x₂ とし、力 F で引っ張るとします。
それぞれのばね定数を k₁ 、k₂ 、伸びを x₁ 、x₂ とし、力 F で引っ張るとします。 重い荷物を持つ場合は2人で持てば半分の力で済みます。
重い荷物を持つ場合は2人で持てば半分の力で済みます。 2人対1人で綱引きをすれば2人の方が勝ちます。
2人対1人で綱引きをすれば2人の方が勝ちます。 つまり同じばねを2つ並列につなげると、1つのときに比べて倍の力が必要です。ばねは伸びにくくなるのです。2つで1つのばねと見なしたときのばね定数は2倍になります。
つまり同じばねを2つ並列につなげると、1つのときに比べて倍の力が必要です。ばねは伸びにくくなるのです。2つで1つのばねと見なしたときのばね定数は2倍になります。 (左図のような装置では実際に引っ張った際には硬いばねの方にワイヤーが片寄ってしまいますが、ここでは理論上、片寄らないで両方とも同じ長さだけ伸ばされることとします。)
(左図のような装置では実際に引っ張った際には硬いばねの方にワイヤーが片寄ってしまいますが、ここでは理論上、片寄らないで両方とも同じ長さだけ伸ばされることとします。)
