弾性力による位置エネルギー
ばねの先に物体を取り付けて、引き伸ばしてから離すと、物体は勢いよく引き戻されます。勢いのついた物体は他の物体に当たれば仕事をすることができるので、エネルギーを持っているといえます。この、引き伸ばされたばねの先に取り付けられた物体の持つエネルギーを弾性力による位置エネルギーといいます。（ここまでは『重力による位置エネルギー』と同じ考え方です。）
ばねを引き伸ばせば伸ばすほど、他の物体への影響は大きそうです。また、物体の質量が大きければ大きいほど、影響は大きそうです。弾性力による位置エネルギーは、ばねの伸びと物体の質量に関係がありそうだということが予想されます…、といいたいところですが、実は物体の質量には関係ありません。物体の質量が大きいとぶつかるときの影響は大きくなりますが、その前段階として、質量が大きいと動かしにくくなるのでスピードは上がらず、トータルでプラマイゼロとなります。『重力による位置エネルギー』での重力 mg は質量 m が大きくなるほど大きくなりましたが、今回は違うのです。今回、位置エネルギーに関係してくるのは、実は、ばねの力強さ（＝ばねの伸びにくさ＝ばね定数）です。ばね定数の大きいばねを大きく伸ばすと弾性力による位置エネルギーは大きくなります。
では、この弾性力による位置エネルギーの大きさを決めるにはどうしたらいいでしょうか。『運動エネルギー』、『重力による位置エネルギー』と同じように、他の物体にぶつかる瞬間から止まる瞬間までの仕事の大きさから定義したいところですが、ばねの場合、ばねの伸びによって刻々と力の大きさが変わるので難しいです。ですので今回は、基準点からばねを伸ばしたときの仕事の大きさから弾性力による位置エネルギーの大きさを定義することにします。これは『重力による位置エネルギー』でも述べましたが、エネルギーの原理が弾性力による位置エネルギーにも適用できるものとして、「物体にされた仕事は弾性力による位置エネルギーの変化量に等しい」ということから、エネルギーを求めるものであります。物体を基準点から x 点まで引き伸ばす際の仕事の大きさを、弾性力による位置エネルギーとするのです。＊ばねを「ゆっくり」伸ばすときの力の大きさは、物体の質量に無関係です。しかし、重力による位置エネルギーを考える際に、物体を持ち上げるとき、質量は大いに関係あります。
というわけで、
重力による位置エネルギーの式 U = mgh には m が含まれていて、
弾性力による位置エネルギーの式 U = \(\large{\frac{1}{2}}\)k x2 には m が含まれていないのです。
閉じる
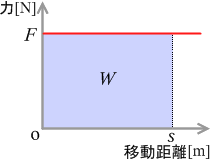『仕事』において、仕事は左図の水色の部分の面積であると説明しました。しかしこれは力が一定の場合の話です。
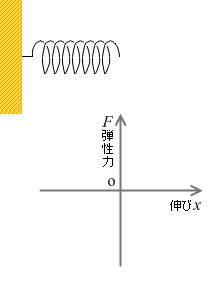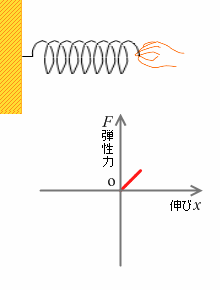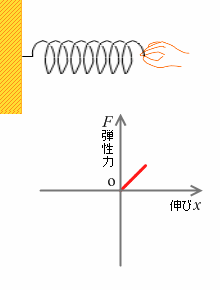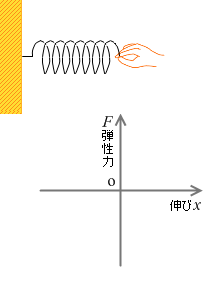ばねというものは『フックの法則』で説明したとおり、伸ばせば伸ばすほど力が大きくなります。
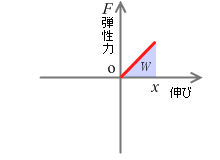ですので、ばねを基準点から x 点まで伸ばすときの仕事の大きさは、左図の水色の三角形部分の面積となります。
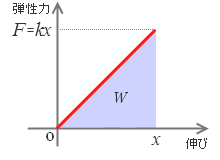図を拡大して水色の部分の面積を計算します。
x だけ伸ばしたときの弾性力は F = k x なので、面積 W は、
W = \(\large{\frac{1}{2}}\)Fx = \(\large{\frac{1}{2}}\)(k x)・x = \(\large{\frac{1}{2}}\)k x2
これが x 点での位置エネルギーです。
弾性力による位置エネルギー
U = \(\large{\frac{1}{2}}\)k x2
単位は仕事や運動エネルギーや重力による位置エネルギーと同じく [J] です。量記号は、重力による位置エネルギーと同じく、W ではなく U を使うことが多いです。質量を表す m は出てきません。弾性力による位置エネルギーは質量とは無関係です。ばねの力強さ（＝ばね定数）とばねの伸びに関係するのです。
ばねの、解放直前のエネルギーは、そこまで伸ばした（あるいは縮めた）際に要した仕事と同じです。
また、弾性力による位置エネルギーのことを単に弾性エネルギーと呼ぶことがあります。この２つの言葉は、ばねの先に取り付けた物体に宿るエネルギーが「弾性力による位置エネルギー」で、ばね自体に宿るエネルギーが「弾性エネルギー」である、と使い分ける場合もあります。しかし、ばねと物体はくっついているわけですから使い分けることにあまり意味はありません。