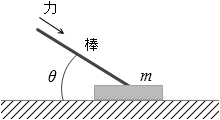
水平な床に質量 m の物体が置かれている。図4のように、物体に棒を取り付け、棒と床のなす角度を θ として、棒の方向に力を加えた。力の大きさを徐々に大きくしていったところ、その大きさが F を超えたとき物体が動き始めた。F はいくらか。ただし、棒の質量は無視できるものとし、物体と床の間の静止摩擦係数を μ 、重力加速度の大きさを g とする。
#センター08追試
水平な床に質量 m の物体が置かれている。図4のように、物体に棒を取り付け、棒と床のなす角度を θ として、棒の方向に力を加えた。力の大きさを徐々に大きくしていったところ、その大きさが F を超えたとき物体が動き始めた。F はいくらか。ただし、棒の質量は無視できるものとし、物体と床の間の静止摩擦係数を μ 、重力加速度の大きさを g とする。
#センター08追試
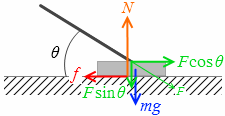F の方向は棒の方向であり斜め方向です。鉛直方向と水平方向に分解すると、
鉛直方向：Fsinθ
水平方向：Fcosθ
垂直抗力 N の大きさは
N = Fsinθ + mg
よって、最大静止摩擦力を f とすると
f = μN = μ(Fsinθ + mg)
物体が動き出す瞬間は Fcosθ と最大静止摩擦力 f が同じ大きさとなっているから
Fcosθ < f の間は動かず、
Fcosθ > f となると動きます。
徐々に大きくしていって動き出す瞬間というのは
Fcosθ = f となる瞬間です。
、
Fcosθ = f
⇔ Fcosθ = μ(Fsinθ + mg)
∴ Fcosθ - μFsinθ = mgμ
∴ F(cosθ - μsinθ) = mgμ
∴ F = \(\large{\frac{mgμ}{\cosθ - μ\sinθ}}\)
(余談)
θ が大きいと、cosθ が小さくなり sinθ が大きくなるので、分母が小さくなり、F は大きくなります。棒の角度が立っているときほど、大きい力が必要ということです。θ の値によっては分母が 0 に近くなり、F がとてつもなく大きくなってしまいます。これは、いくら力を入れても動かないということです。