qO9E5

AさんとBさんが浮力に関する探究活動を行っている。後の問い（問1～5）に答えよ。

Aさん：ばねはかりを買ったので、ジャガイモで浮力の実験をしてみよう。
Bさん：ジャガイモは水に沈むので、水より密度は大きいはずだね。
Aさん：密度と浮力の関係を確認しておこう。

　

（問1）密度 2.0×103kg/m3、質量 1.0kg の物体が水中に完全に沈んでいるとき、物体にはたらく浮力の大きさはいくらか。ただし、水の密度を 1.0×103kg/m3、重力加速度の大きさを 9.8m/s2 とする。

　

Aさん：糸でジャガイモをばねはかりにつるし、水を入れた計量カップに徐々に沈めてみよう。
Bさん：ジャガイモの下端Pの水面からの深さと、ばねはかりの値から、浮力の変化がわかるんじゃないかな?
Aさん：そうだね。Pが水面より上にあるときは深さを負の値とすればいいね。せっかくなので計量カップの下にキッチンはかりを置いて実験してみようよ。

図1のようにAさんとBさんの二人は、水を入れた計量カップとジャガイモを用いて実験を行った。

図 1

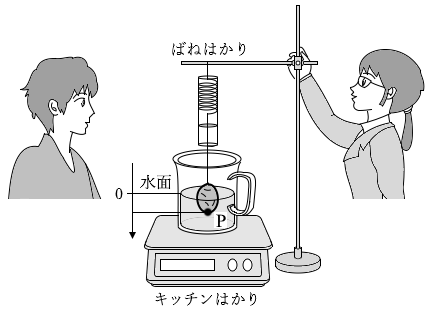
AさんとBさんは、結果を図2の二つのグラフにまとめて議論している。

　

（問2）次の会話文中の空欄ア・イには、それぞれ直後の｛ ｝内の数式および値のいずれか一つが入る。入れる数式および値を示す記号の組合せとして最も適当なものを、後の①～⑨のうちから一つ選べ。ただし、糸の質量と体積は無視できるものとする。

Aさん：ジャガイモが計量カップの底についていないとき、ジャガイモにはたらく力について考えてみよう。
Bさん：ジャガイモにはたらく力は浮力と重力と糸の張力だね。
Aさん：浮力の大きさを \(F\)、重力の大きさを \(W\)、張力の大きさを \(T\) とすると、
ア｛ (a) \(F=T+W\)　(b) \(F=T-W\)　(C) \(F=W-T\) ｝の関係があるね。
Bさん：図2の上のグラフから読み取るとジャガイモ全体が水に沈んだときの浮力の大きさは、約イ｛ (d) 0.1　(e) 1.0　(f) 1.1 ｝Nだね。

① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨
ア (a) (a) (a) (b) (b) (b) (C) (C) (C)
イ (d) (e) (f) (d) (e) (f) (d) (e) (f)

　

図 2

Aさん：図2の二つのグラフでは、キッチンはかりの値が大きくなるとばねはかりの値は小さくなるね。
Bさん：その関係をグラフで表してみよう。

　

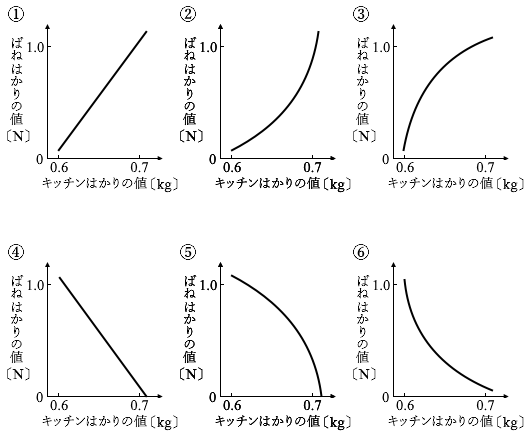
（問3）ばねはかりの値とキッチンはかりの値の関係を表すグラフとして最も適当なものを、次の①～⑥のうちから一つ選べ。

　

　

Aさん：図2の上のグラフを見ると、ジャガイモを水に沈めていく間は、ばねはかりの値の変化が直線的ではなく曲線になっているけど、なぜかな?
Bさん：横軸の目盛りが 0~5cm あたりのところだね。ジャガイモの形が関係しているのかもしれないね。
Aさん：ジャガイモの代わりに、いろいろな形の物体で確かめてみればわかるね。

　

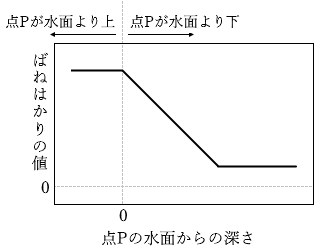
（問4）水より密度の大きい一様な材質でできたある形の物体をつるして、図1と同じような実験をした。すると、ばねはかりの値と点Pの水面からの深さとの関係を表すグラフが、次の図3のようになった。このとき、その物体とつるし方として最も適当なものを、後の①～④のうちから一つ選べ。

図 3

　

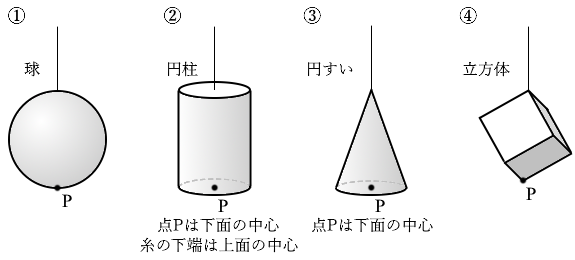
（問5）次の会話文中の空欄ウ・エにはそれぞれ直後の｛ ｝内の語句のいずれか一つが入る。入れる語句を示す記号の組合せとして最も適当なものを、後の①～⑨のうちから一つ選べ。

Aさん：ジャガイモが計量カップの底について糸が緩んでいるときに、ジャガイモにはたらいている力はどうなっているのかな？
Bさん：ジャガイモにはたらく力は、計量カップの底からはたらく垂直抗力と
ウ｛ (a) 重力　(b) 重力と浮力　(C) 重力と張力 ｝だね。
Aさん：そうすると、ジャガイモに計量カップの底からはたらく垂直抗力は、
水がない場合と比べると、エ｛ (d) 大きくなる　(e) 同じ大きさだ　(f) 小さくなる ｝ね。

① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨
ウ (a) (a) (a) (b) (b) (b) (C) (C) (C)
エ (d) (e) (f) (d) (e) (f) (d) (e) (f)

#共テ24本試物理基礎

（問1）
浮力というものは、流体の密度と物体の体積と重力加速度をかけたものです（\(F = ρVg\)）。

まず物体の体積（\(V\)）を求めますと、質量を密度（\(ρ\)）で割って

　　\({\large\frac{1.0}{2.0×10^3}}\) [m3]

これに流体の密度と重力加速度（\(g\)）をかけて浮力を求めますと

　　\(1.0×10^3 × {\large\frac{1.0}{2.0×10^3}} × 9.8\) = 4.9 [N]

　

　

（問2）
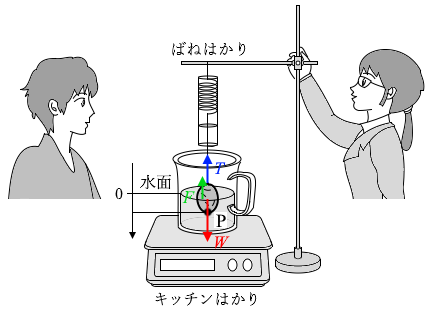浮力 \(F\) は上向き、重力 \(W\) は下向き、張力 \(T\) は上向きであり、ジャガイモは加速しているわけではないのでこれらの力はつり合っています。つまり

　　\(F + T = W\)

でありますのでアの答えは上式を移項して (C) \(F=W-T\)

\(F=W-T\) のうち重力 \(W\) はずっと変わらないものですが、浮力 \(F\) はジャガイモが沈んでいくほど排除する水のかさが増えていきますので大きくなっていきます。それにともなって張力 \(T\) は小さくなっていきます。

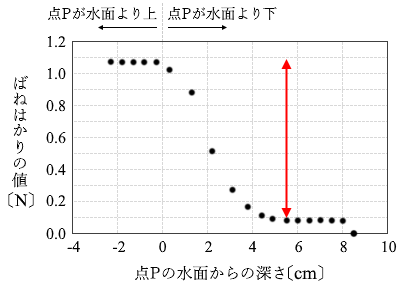ジャガイモが沈みきってしまえばそれ以上浮力は増えない、つまり張力（＝ばねはかりの値）は一定になるはずで、グラフから読み取ると 4.8cm くらい沈めたところでそのようになっています。

そして沈める前と比べると (e) 1.0N くらい軽くなっています。軽くなったのは浮力によるものです。

答えは ⑧ です。

　

　

（問3）
計量カップと水とジャガイモの3つの重さを支えているのは、ばねはかりとキッチンはかりの2つだけです。ばねはかりの負担が軽くなればその分キッチンはかりの負担が重くなります。ばねはかりの値を \(T\)、キッチンはかりの値を \(K\) とおくと　\(T + K = 一定\)　です。移項すると　\(T = - K + 一定\)　です。これを表す\(T\)-\(K\)グラフの曲線は傾きが負で一定になります。つまり答えは ④ です。

この問題を解く上で浮力がトータルの重さに関係してくると感じてしまう方はまだ作用反作用の法則が理解できていません。浮力がジャガイモを上に押すと同時にジャガイモが水を下に押すのでトータルでは変化がないのです。計量カップと水とジャガイモの3つの合計の重さは変わらないのです。ばねはかりの負担が軽くなった分は必ずキッチンはかりの負担になります。

たとえば、100g のビーカーの中で 10g の蝶が止まっている場合、はかりは 110g を指しますが、蝶がビーカーの中で羽ばたいたときも、はかりは 110g を指します。蝶が浮き上がったからといって 100g にはなりません、110g です。作用反作用により、10g の蝶を浮き上がらせればその 10g の分、ビーカーを下に押します。内部で起こっていることはトータルの重さに関係しないのです。

　

　

（問4）
ばねはかりの値が徐々に小さくなるということは浮力が大きくなっていくということですが、浮力の大きさというのは排除した水の体積によります。

グラフを見ると直線的に小さくなっていっていますので、沈めていく過程で物体の体積が大きくなったり小さくなったりしないもののはずです。そのような形の物体は ② の円柱です。

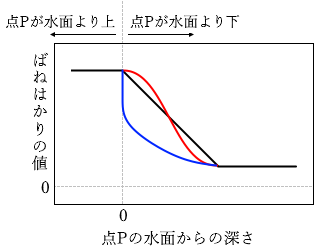もし球であれば左図の赤線のような曲線になるだろうし、円すいなら青線のようになるはずです。ジャガイモの場合を表す図2のグラフは赤線のようになってます。

　

　

（問5）
糸が緩んだということは張力がいっさいはたらいていないということです。ですからジャガイモにはたらく力は垂直抗力と (b) 重力と浮力 の3つです。ジャガイモが底についたら浮力がはたらかないのではないかと思われるかもしれませんが、ジャガイモの下に水分子が1個でももぐり込めれば浮力ははたらきます。詳しくは『軽い物体が水底にある場合』をご覧ください。

そして、浮力がはたらいていればジャガイモが計量カップの底を押す力も弱まりますのでそれに対抗する垂直抗力も (f) 小さくなり ます。

答えは ⑥ です。