作用⋅反作用の法則
押すと押し返される
空気を押しても手応えは感じません。
のれんを押せばわずかに手応えを感じます。
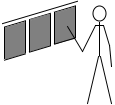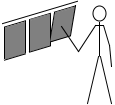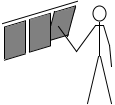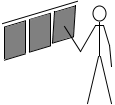のれんが鉄でできていればまあまあの手応えを感じます。
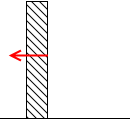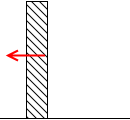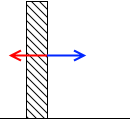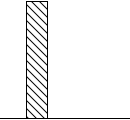コンクリートの壁を押せば強い手応えを感じます。
このように手応えを感じるのは押し返されるからです。
左図の青矢印のような、面に垂直な押し返す力を垂直抗力といいます。実際には押す力と押し返す力は時間差はありません、同時に発生します。左図は説明のために時間差をもうけて表現しました。＊
力に時間差があると考えるのはナンセンスですし、力に押す力と押し返す力があると考えるのも本当はナンセンスです。力には主と従、あるいは原因と結果のような関係はなく、いつも対等で同時にはたらく、と考えるのが物理的センスのいい考え方です。
閉じる
押すときだけでなく引っ張るときも抵抗するかのような力を感じます。
杭が無かったら？
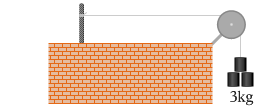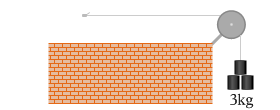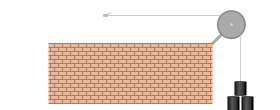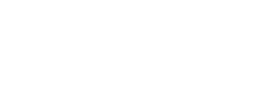
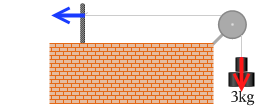
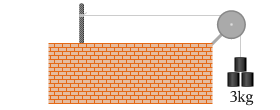左図は、台に滑車が取り付けられていて、ロープの片方が杭に固定されていて、もう片方に重りが吊り下げられている場面を示しています。
いま 3.0kg の重りが吊り下げられ静止しているとします。
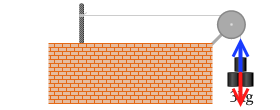静止しているということはつり合っているということだから、赤色の重力 3.0×9.8[N] の力と上向きの青色の力は同じ大きさ、つまり 3.0×9.8[N] ということになるはずです。
この青色の力はどこから来たものでしょうか。
いま急に、杭が無くなったとすると重りは下へ落ちていってしまいますが、
仮にもし、もう片方の端に滑車があるとすると何kgの重りがあれば静止させることができるでしょうか？それはもちろん 3.0kg です。これはつまり、杭が存在することと、もう片方に 3.0kg の重りが吊り下げられることとは、同等ということです。
すなわち、杭が 3.0×9.8[N] で引っ張っていたのです。青色の力は杭が引っ張っている力なのです。＊杭はロープに引っ張られているわけですが、杭が動かないのは、台が杭を固定しているからです。台を形成する分子たちが、杭がもぎ取られないように踏ん張っているからです。固体の物体は分子間力によって形が保たれてます。
閉じる
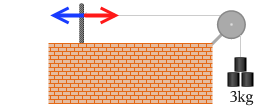力の関係を重りに着目せず、杭とロープの結び目に着目すると、左図のようになります。この図の意味は、ロープが杭を 3.0×9.8[N] で引っ張り、杭がロープを 3.0×9.8[N] で引っ張り返しているという意味です。
作用⋅反作用の法則
押すと押し返され、引っ張ると引っ張り返されることを作用⋅反作用の法則＊「⋅」はあっても無くてもかまいません。「作用⋅反作用の法則」でも「作用反作用の法則」でもOKです。
閉じるといいます。対になっている２つの力は、大きさが等しく、向きが反対で、同一作用線上にあります。前項の力のつり合いの条件とそっくりです＊その区別はちょっとややこしいです。
閉じる。
今まで力に関してこのようなことは意識して来なかったと思いますが、物理ではとても重要なことです。この原理から運動量保存の法則というものが導き出されたり＊あるいは運動量保存の法則から作用⋅反作用の法則が導き出されるとも考えられます。
閉じる、力というものが定義されたりします。地味ですが本当に重要なものです。
この作用⋅反作用の法則は運動の第3法則とも呼ばれています。かの有名なニュートンが発見しました。後で、運動の第1法則、運動の第2法則というものも学びます。
改めて、力とは
力というものは交換されるものであり、必ず相手が必要です＊空気を押す場合も腕に力が入っているかもしれませんが、それは空気に対してというよりも筋肉細胞同士の押し合いや引っ張り合いに使われているといえます。
また、
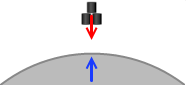自由落下運動している物体に掛かる重力（万有引力）は単独で存在しているのではなく、物体と地球の間で相互に作用しているものです。
電場の中に置かれた電荷も力を受けますが、これは、電場には発生源があり、電荷と発生源が相互に作用し合っているのであって、力が単独で存在しているわけではありません。
閉じる。その大きさはどちらかが大きいということはなく必ず同じ大きさです＊ですから本当のところは、一方が「作用」で他方が「反作用」というようなことはありません。
閉じる。力というものは必ず対になって作用し、等価交換されるものです。
このことが実感しにくいのは地上においては多くのものが固定されているからです。ものが動かないので力が一方通行であるかのように感じてしまいます。
宇宙空間にプカプカ浮いているもの同士であれば、力を加えたときに自分も相手も動きます。宇宙飛行士は作用⋅反作用の法則を体で理解しているはずです。
同一作用線上
同一作用線上という言葉に関して断っておきますが、右図のような青色と赤色の2つの力も同一作用線上にある、といえます。ピンと張られたロープは力を均一に伝えるからです。ロープがピンと張っている場合は曲げられていても同一作用線上にあるといってかまいません。
作用⋅反作用の法則の例
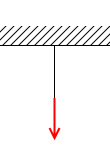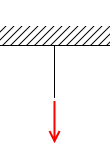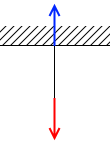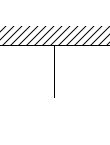天井から吊るされたロープを引っ張ると天井は同じ大きさの力で引っ張り返します。＊これも作用の力と反作用の力に時間差があるわけではありません。時間差をもうけたのは説明のための演出です。
閉じる
なめらかな床の上に物体が置かれていて、それを押しても動かないとき、物体には大きさが同じで向きが反対の力がはたらいています。
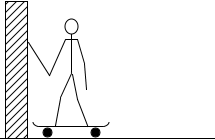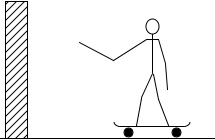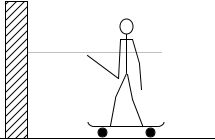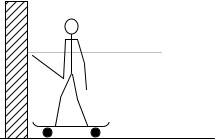スケボーに乗った人が壁を押すと押し返されます。ロープを引っ張ると引っ張り返されます。
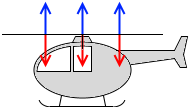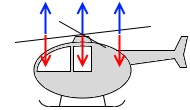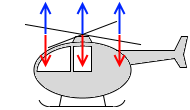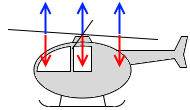ヘリコプターは空気を下に押していて、その反作用として空気がヘリコプターを上に押し上げています。ホバリングしているヘリコプターの重さが 10㌧であったとすれば、ヘリコプターは10㌧分の反作用の力を受けています。
作用⋅反作用の法則は動いているときもはたらく
作用⋅反作用の法則は物体が動いているときもはたらきます。
宇宙空間に浮かぶ鉄球を手で力を加えて動かすとき（加速させるとき）、手は反作用の力を受けます。＊このとき鉄球の質量が 2kg であっても 3kg であっても加える力が 10N であれば反作用の力も 10N です。たとえ鉄球が 1mg であったとしても加える力が 10N なら反作用も 10N です。（1mg の鉄球に 10N もの力を加えたら銃弾のように飛んでいきますが）
閉じる（等速で動いているのであれば力は加わっておらず、作用⋅反作用の法則ははたらきません。詳しくは『慣性の法則』項や『運動方程式』項をご覧ください。）
自由落下している最中の物体も、地球との間で作用⋅反作用の法則がはたらいています。
以下はちょっと難しい話ですが、
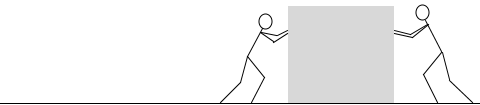力の弱い人と力の強い人が押し合ったとき、
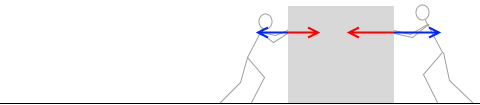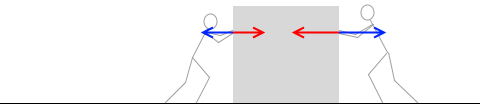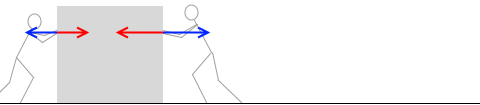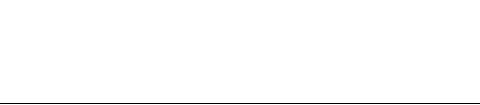40N で押した人は 40N の反作用の力、60N で押した人は 60N の反作用の力を受けます。物体がどちらに動こうとも、あるいは動かなくても、加えた力と同じ大きさの反作用の力を受けます。40N+60N で 100N の反作用の力を受けるというようなことはありません。
物体に関しては摩擦が無ければ 20N の力を受けて加速していきます。
（この場合、等速で動いていたとしても、あるいはつり合って静止していたとしても、力は加わっているので作用⋅反作用の法則ははたらきます。）