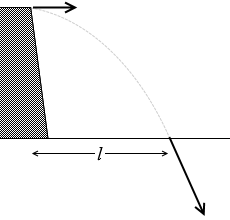
高さ 19.6m の崖の上から、小石を水平方向に速さ 10m/s で投げ出した。空気抵抗は無視できるものとし、重力加速度の大きさを 9.8m/s2 として、以下の問いに答えよ。
(1) 小石を投げ出してから地面に衝突するまでの時間 t [s] はいくらか。
(2) 衝突地点までの水平距離 l [m] はいくらか。
(3) 小石が衝突する直前の速度の大きさ v [m/s] はいくらか。
高さ 19.6m の崖の上から、小石を水平方向に速さ 10m/s で投げ出した。空気抵抗は無視できるものとし、重力加速度の大きさを 9.8m/s2 として、以下の問いに答えよ。
(1) 小石を投げ出してから地面に衝突するまでの時間 t [s] はいくらか。
(2) 衝突地点までの水平距離 l [m] はいくらか。
(3) 小石が衝突する直前の速度の大きさ v [m/s] はいくらか。
(1)
水平投射の鉛直方向の式は、高さを y とすると y = \(\large{\frac{1}{2}}\)gt2 だから、
19.6 = \(\large{\frac{1}{2}}\)×9.8×t2
∴ t2 = \(\large{\frac{19.6}{9.8}}\)×2
⇔ t2 = 2×2
∴ t = 2.0 [s]
(2)
水平方向へは鉛直成分と無関係に初速のスピードのまま飛んでいきます。そしてその時間が t = 2.0 [s] であるわけですから、
l = 10×2.0
= 20 [m]
(3)
水平方向の速さを vx とするとそれは初速と同じだから、
vx = 10 [m/s]
鉛直方向の速さを vy とすると y = gt だから、
vy = 9.8×2.0 = 19.6 [m/s]
速度ベクトル \(\vec{v}\) の大きさ v は
v = \(\sqrt{{v_x}^2+{v_y}^2}\) = \(\sqrt{10^2+19.6^2}\) = \(\sqrt{100+384.16}\)= \(\sqrt{484.16}\)
≒ 22 [m/s]