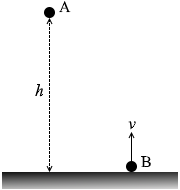
図3のように、高さ h の位置から小物体Aを静かに離すと同時に、地面から小物体Bを鉛直上方に速さ v で投げ上げたところ、二つの小物体は同時に地面に到達した。v を式で表せ。ただし、二つの小物体は同一鉛直線上にないものとし、重力加速度の大きさを g とする。
#センター13本試
図3のように、高さ h の位置から小物体Aを静かに離すと同時に、地面から小物体Bを鉛直上方に速さ v で投げ上げたところ、二つの小物体は同時に地面に到達した。v を式で表せ。ただし、二つの小物体は同一鉛直線上にないものとし、重力加速度の大きさを g とする。

#センター13本試
小物体Aが地面に到達するまでの時間を t として、自由落下運動の変位の式を立てますと、
h = \(\large{\frac{1}{2}}\)gt2
∴ t2 = \(\large{\frac{2h}{g}}\)
∴ t = \(\sqrt{\frac{2h}{g}}\) ……①
小物体Bが投げ上げられてから地面に到達するまでの時間も t であり、鉛直上方投射の変位の式を立てますと、
0 = vt - \(\large{\frac{1}{2}}\)gt2
∴ 0 = v - \(\large{\frac{1}{2}}\)gt
∴ \(\large{\frac{1}{2}}\)gt = v
∴ t = \(\large{\frac{2v}{g}}\) ……②
② = ① だから、
\(\large{\frac{2v}{g}}\) = \(\sqrt{\frac{2h}{g}}\)
∴ v = \(\sqrt{\large{\frac{gh}{2}}}\)
(余談)
慣れてる人は
h = \(\large{\frac{1}{2}}\)gt2
- v = v - gt
という式を立ててもいいと思います。