長さ L の質量が無視できる棒の一端を、鉛直面内でなめらかに回転できるように支点に取り付け、他端におもりを取り付けた。支点の鉛直上方でおもりを静かに離すと、棒は重力によって鉛直面内で図2のように反時計回りに回転し始めた。鉛直上方から測った棒の角度 θ とおもりの速さ v との関係を表すグラフとして最も適当なものを、下の①～④のうちから一つ選べ。ただし、グラフには 0° < θ ≦ 180° の範囲が示されている。重力加速度の大きさを g とし、空気の影響は無視できるものとする。
#センター11本試
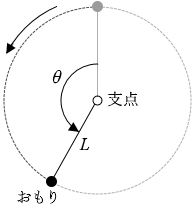
摩擦が無いので力学的エネルギー保存の法則が成り立っているはずです。おもりの質量を m 、90°の位置でのおもりの速さを v90 、180°の位置でのおもりの速さを v180 、最下点を位置エネルギーの基準位置としますと、
最上点での力学的エネルギーは
（運動エネルギー）+（位置エネルギー）=（\(\large{\frac{1}{2}}\)m⋅02）+（mg2L） ……➊
90°の位置での力学的エネルギーは
（運動エネルギー）+（位置エネルギー）=（\(\large{\frac{1}{2}}\)mv902）+（mgL） ……➋
最下点での力学的エネルギーは
（運動エネルギー）+（位置エネルギー）=（\(\large{\frac{1}{2}}\)mv1802）+（mg⋅0） ……❸
力学的エネルギー保存の法則より➊=➋であるから、
（mg2L）=（\(\large{\frac{1}{2}}\)mv902）+（mgL）
∴ 2gL = \(\large{\frac{1}{2}}\)v中2 + gL
∴ \(\large{\frac{1}{2}}\)v902 = gL
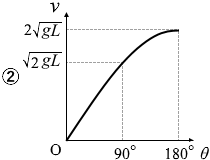
∴ v90 = \(\sqrt{2gL}\)
さらに、力学的エネルギー保存の法則より➊=❸であるから、
（mg2L）=（\(\large{\frac{1}{2}}\)mv1802）
∴ g2L = \(\large{\frac{1}{2}}\)v1802
∴ 4gL= v1802
∴ v180 = 2\(\sqrt{gL}\)
v90 = \(\sqrt{2gL}\) 、v180 = 2\(\sqrt{gL}\) となっているグラフは ② です。
（もうちょっと一般化して考えてみる）
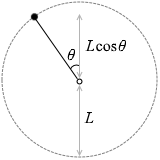角度が θ のときのおもりの高さは
L + Lcosθ
であり、この位置での力学的エネルギーは
（運動エネルギー）+（位置エネルギー）=（\(\large{\frac{1}{2}}\)mv2）+（mg(L + Lcosθ)） ……❹
力学的エネルギー保存の法則より➊=❹であるから、
（mg2L）=（\(\large{\frac{1}{2}}\)mv2）+（mg(L + Lcosθ)）
∴ g2L = \(\large{\frac{1}{2}}\)v2 + g(L + Lcosθ)
∴ g(L - Lcosθ) = \(\large{\frac{1}{2}}\)v2
∴ 2gL(1 - cosθ) = v2
∴ v = \(\sqrt{2gL(1-\cosθ)}\)
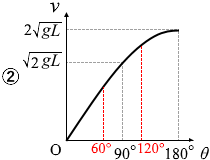この式に θ = 60° を代入してみますと、
v60 = \(\sqrt{2gL(1-\frac{1}{2})}\) = \(\sqrt{gL}\)
θ = 120° を代入してみますと、
v120 = \(\sqrt{2gL(1+\frac{1}{2})}\) = \(\sqrt{3gL}\)
これらの値は、②のグラフにマッチしています。
（勘違いしやすい）
本問で示されたグラフは、横軸が θ です。t ではありません。横軸が t であると思い込むと思わず③が妥当ではないかと勘違いしてしまいます。
また、この運動は単振動とも別物です。単振動は等速円運動を射影した動きです。グラフの曲線は正弦波（サインカーブ）ではありません。本問の運動は力学的エネルギーが保存されるような特徴を持った運動です。ジェットコースターの動きに近い運動です。