単振動
単振動
物体の運動を考えるとき、基本的なものといえば、静止、等速直線運動、等速円運動です。このうち等速直線運動は時間が経つにつれて物体が遠くに行ってしまう運動ですが、等速円運動は遠くには行ってしまわない運動です。この世の物がすべて遠くに行ってしまうとこの世は成り立ちません。この世が成り立っているということは物体が静止しているか、等速円運動になぞらえられる周期的な運動をしているからです。
直線上の運動ではあるけれども等速円運動になぞらえられる運動が単振動という運動です。
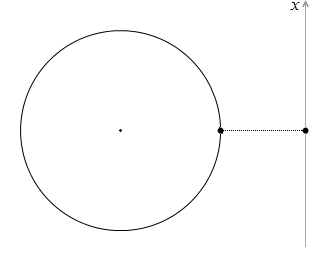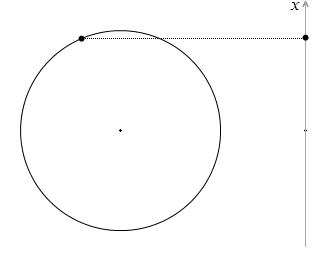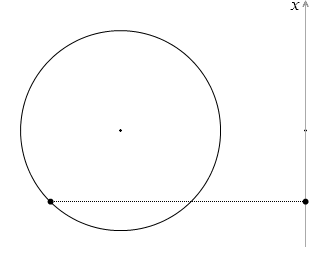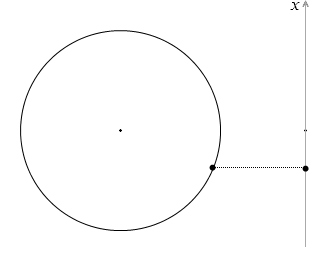 この運動は等速円運動する物体を真横から光を当てて鉛直の壁に射影(正射影といいます)したような往復運動です。あるいは、円の中心を通る鉛直線に射影したような往復運動です。ばねの先に付けたおもりのような動きです。*
この運動は等速円運動する物体を真横から光を当てて鉛直の壁に射影(正射影といいます)したような往復運動です。あるいは、円の中心を通る鉛直線に射影したような往復運動です。ばねの先に付けたおもりのような動きです。*
左側の赤玉の動きは単振動ではありません。ばねっぽさがありません。右側の青玉の動きが単振動です。
閉じる
ですので、
等速円運動の周期を T [s]
角速度を ω [rad/s]
回転数を f [Hz]
円の半径を A [m]
としますと、
単振動の1往復する時間(=周期)も T [s]
1秒当たりの回転角(単振動においては角振動数あるいは角周波数という)も ω [rad/s]
1秒当たりの往復数(単振動においては振動数あるいは周波数という)も f [Hz]
単振動の振幅も A [m] *
『等速円運動』では量記号に r を用いてました。単振動や『波動』では A を用いることが多いです。
A は amplitude(振幅) から。大文字を使うのはたぶん加速度の a と間違えないようにするため。
振幅というのは円の直径部分でなく円の半径部分に相当することに注意してください。
閉じる
となります。
角振動数と振動数の微妙な違いに気を付けてください。たとえば角振動数が \(\large{\frac{\pi}{2}}\)rad/s だった場合には振動数は \(\large{\frac{1}{4}}\)Hz です。1秒当たり90°回転するとき1秒当たり \(\large{\frac{1}{4}}\) 往復する、ということです。角振動数が π rad/s のときは振動数は \(\large{\frac{1}{2}}\)Hz です。f = \(\large{\frac{\omega}{2\pi}}\) です。(『円運動』項では f の替わりに n を使ってました)
「振動数」、「周波数」、「回転数」、「1秒当たりの往復数」の4つに関しては同じ意味ととらえてもらって差し支えありません。「角振動数」は「角速度」と同じです。
等速円運動と単振動と正弦波
単振動は、正弦波と密接な関係がある運動です。等速円運動と単振動と正弦波は密接な関係があります。これらにおいては以下の式が一般的に成り立ちます。
f = \(\large{\frac{1}{T}}\)
ω = 2πf = \(\large{\frac{2\pi}{T}}\)
単振動の変位
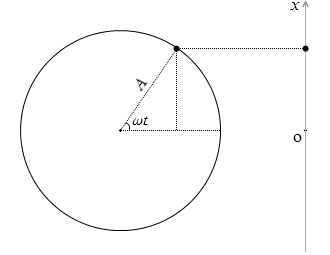 単振動する直線を x軸とし、振動の中心を x = 0 、t = 0 としますと、
単振動する直線を x軸とし、振動の中心を x = 0 、t = 0 としますと、
単振動の変位 x [m] は A に sinωt を掛けたものです。(角度が ωt で、それの sin が A と x の長さの比です)
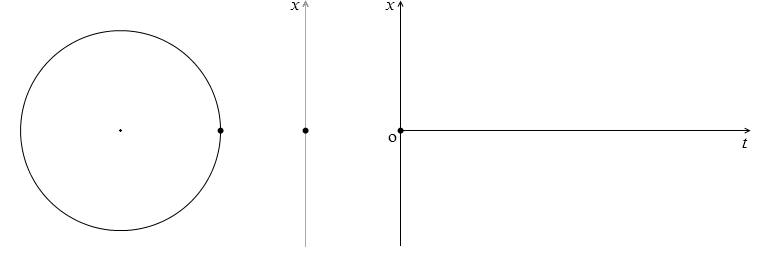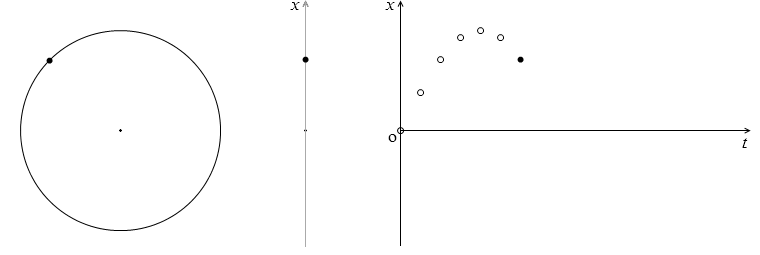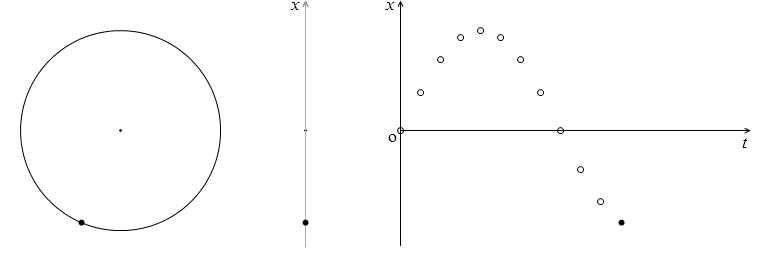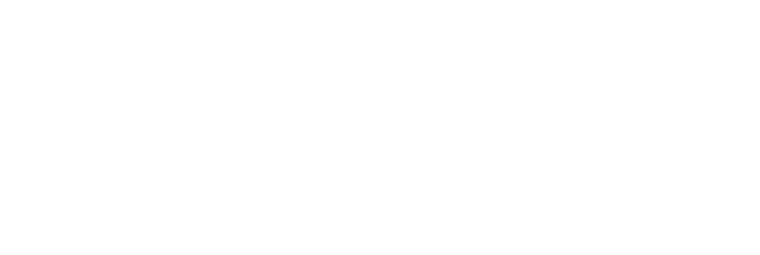
単振動の変位
x = Asinωt
上図の右のグラフは上式をグラフで表したものであり、この形の曲線を正弦曲線といいます。正弦波の形と同じです。
波のグラフを見るときは、横軸が x であるか t であるかを確認することが大事ですが、上のグラフの横軸は t です。単振動はその場にとどまる動きなので横軸は x にはなりません。もし多くの媒質が連なっていて、そこを進行する波を分析するなら、横軸が x になることもあり得ます。その時も曲線は正弦曲線になります。
単振動の速度
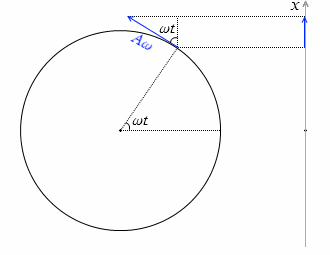 単振動の速度 v [m/s] は等速円運動の速さ Aω を x軸に射影したものです。つまり、Aω に cosωt を掛けたものです。
単振動の速度 v [m/s] は等速円運動の速さ Aω を x軸に射影したものです。つまり、Aω に cosωt を掛けたものです。
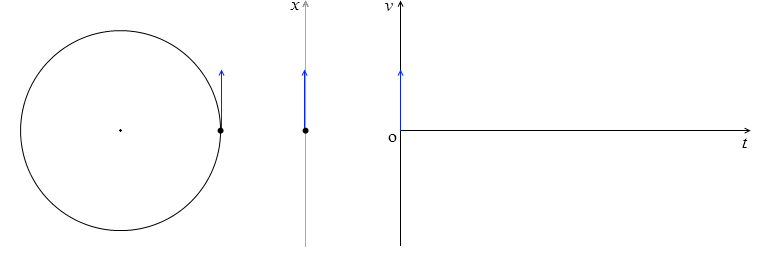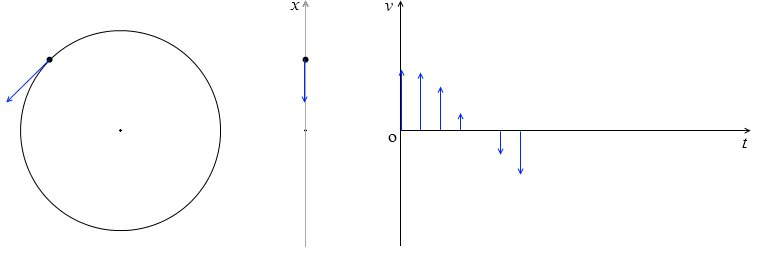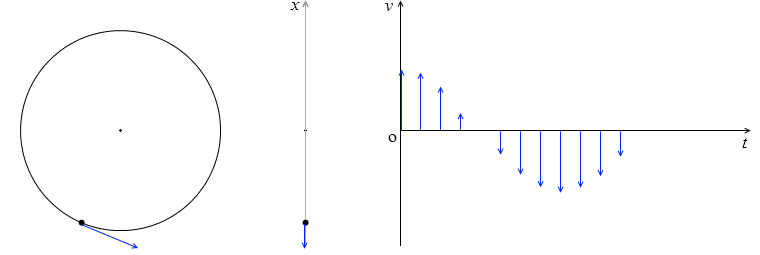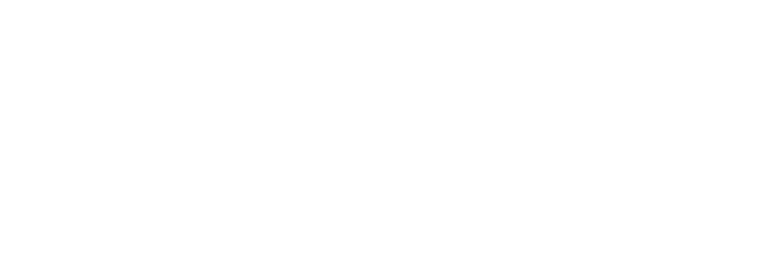
位相 ωt が 0 から \(\large{\frac{\pi}{2}}\) までの間(cosωt > 0 の間)は速度の向きは上向き、つまり v > 0 で、
位相 ωt が \(\large{\frac{\pi}{2}}\) から \(\large{\frac{3}{2}}\pi\) までの間(cosωt < 0 の間)は速度の向きは下向き、つまり v < 0 です。
単振動の速度
v = Aωcosωt
単振動の加速度
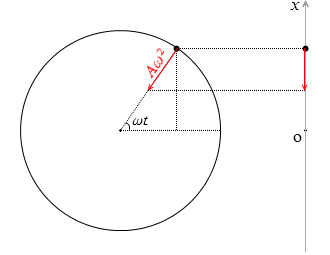 単振動の加速度 a [m/s2] は等速円運動の加速度 Aω2 を x軸に射影したものです。つまり、Aω2 に sinωt を掛けたものです。
単振動の加速度 a [m/s2] は等速円運動の加速度 Aω2 を x軸に射影したものです。つまり、Aω2 に sinωt を掛けたものです。
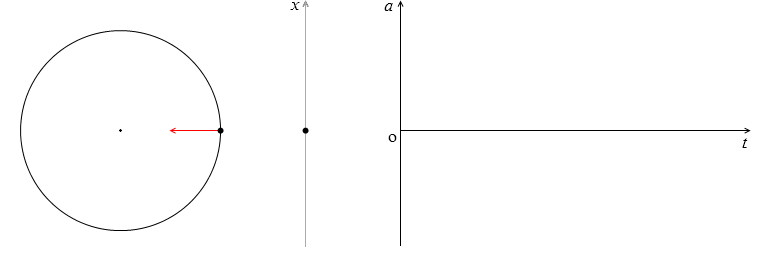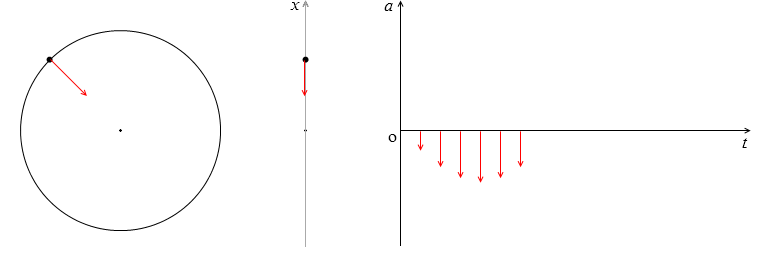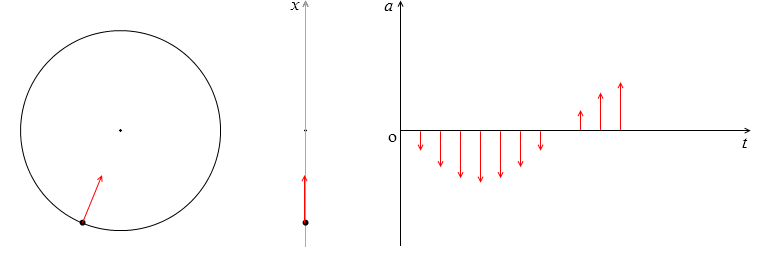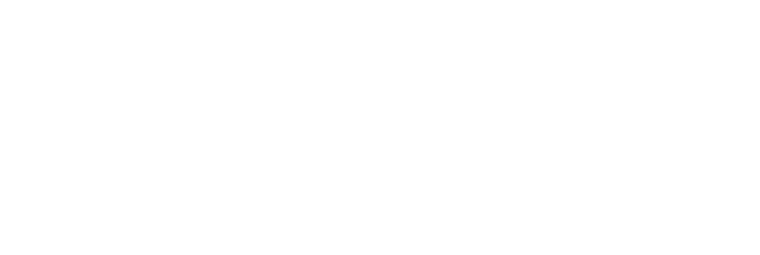
正負について注意が必要なのですが、変位が正のとき加速度が負で、変位が負のとき加速度が正です。上図において物体が中心より上にあるときは加速度は下を向き、物体が中心より下にあるときは加速度は上を向きます。sinωt > 0 のとき a < 0 で、sinωt < 0 のとき a > 0 です。
つまり加速度の式は - を付けて、
a = - Aω2sinωt
となります。この式に上で求めた変位の式 x = Asinωt を代入すると、
a = - ω2x
となります。
単振動の加速度
a = - Aω2sinωt
あるいは
a = - ω2x
変位と速度と加速度のグラフ
三角関数の微分をご存知の方はお分かりかもしれませんが、
変位の式 x = Asinωt を時間微分したものが、
速度の式 v = Aωcosωt で、さらに時間微分したものが、
加速度の式 a = - Aω2sinωt となっています。
それぞれのグラフを示します。
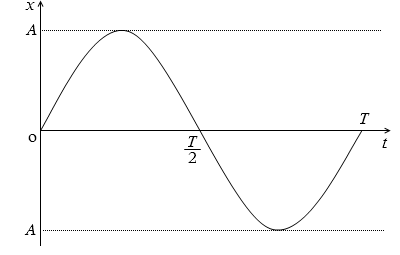
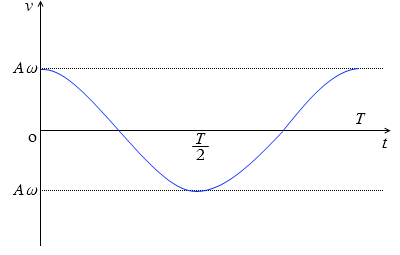 変位の曲線の接線の傾きが速度の曲線になります。変位が 0 のときに速度は最大になります。上のアニメーションで確認してください。
変位の曲線の接線の傾きが速度の曲線になります。変位が 0 のときに速度は最大になります。上のアニメーションで確認してください。
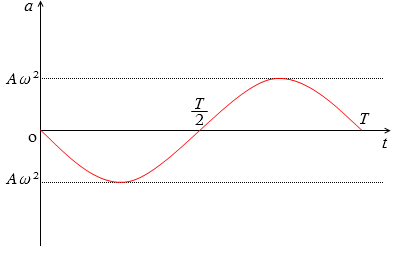 速度の曲線の接線の傾きが加速度の曲線になります。変位と加速度は向きが反対で、変位の絶対値が最大のときに加速度の絶対値も最大になります。
速度の曲線の接線の傾きが加速度の曲線になります。変位と加速度は向きが反対で、変位の絶対値が最大のときに加速度の絶対値も最大になります。
単振動を引き起こす力
質量 m [kg] の物体が単振動しているとき、この物体にはたらいている力 F [N] は運動方程式 ma = F より、
F = ma = m(- ω2x) = - mω2x
です。
上で説明したように、この加速度は変位と逆向きにはたらき、大きさは変位の大きさに比例します。つまり、この力は常に物体を原点に戻そうとするのです。このような力がはたらくとき、物体は単振動するのです*
本項では
「等速円運動の正射影である単振動」 ⇒ 「変位の式と加速度の式を比べると、向きが逆で大きさが比例、つまり復元力が発揮されている。」
ということを説明していますが、その逆が成り立つことを説明していません。本当は説明しなければいけないのですが、次の説明でごまかさせてください。
” 復元力がはたらいているということは、加速度の式と変位の式を比べたときに、マイナスが付いて、大きさが比例、となっている。ある式を2回積分して元の式と比べたときに、マイナスが付いて、大きさが比例となるパターンは sin関数しかなく、sin関数は等速円運動を正射影した単振動を表している。 ”
閉じる。このような特徴を持つ力を復元力といいます。この力は等速円運動における向心力の正射影ともいえます。
復元力の式のうち定数部分 mω2 を K (K > 0)*ドイツ語 Konstant より。
K を小文字で書く場合はばね定数を意味することが多いです。
閉じる に置き換えて表すことがよくあります。
F = - Kx
復元力
F = - mω2x
あるいは
F = - Kx (mω2=K > 0)
F = - ●x の形が出てきたら「単振動」と連想してください。(『ばね振り子』項、『単振り子』項、『振動回路』項参照)
単振動の周期
mω2 を K とおいたので、
ω2 = \(\large{\frac{K}{m}}\)
∴ ω = \(\sqrt{\large{\frac{K}{m}}}\)
すると周期 T [s] は、
T = \(\large{\frac{2\pi}{\omega}}\) = 2π\(\sqrt{\large{\frac{m}{K}}}\)
と表せます。
単振動の周期
T = 2π\(\sqrt{\large{\frac{m}{K}}}\)