図5(a)～(C)のように、ばね定数 \(k\) の軽いばねの一端に質量 \(m\) の小球を取り付け、ばねの伸縮方向に単振動させる。(a)～(C)の場合の単振動の周期を、それぞれ \(T_{\rm a}\) 、 \(T_{\rm b}\) 、 \(T_{\rm c}\) とする。\(T_{\rm a}\) 、 \(T_{\rm b}\) 、 \(T_{\rm c}\) の大小関係として正しいものを、下の ①～⑥のうちから一つ選べ。ただし、(a)の水平面、(b)の斜面はなめらかであるとする。
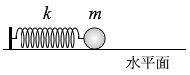
(a) ばねの他端を
水平面上で固定する。
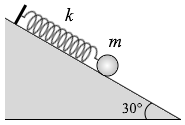
(b) ばねの他端を傾き30°の
斜面上で固定する。
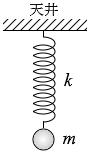
(C) ばねの他端を
天井に固定する。
① \(T_{\rm a} > T_{\rm b} > T_{\rm c}\) ② \(T_{\rm c} > T_{\rm b} > T_{\rm a}\) ③ \(T_{\rm b} = T_{\rm c} > T_{\rm a}\)
④ \(T_{\rm a} = T_{\rm b} = T_{\rm c}\) ⑤ \(T_{\rm a} = T_{\rm c} > T_{\rm b}\) ⑥ \(T_{\rm b} > T_{\rm a} = T_{\rm c}\)
#センター19本試物理
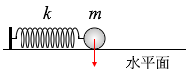(a)のばねには小球にはたらく重力はかかりません。
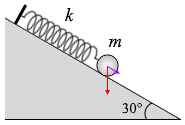(b)のばねには小球にはたらく重力に 
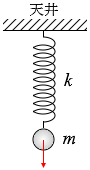(C)のばねには小球にはたらく重力すべてがかかります。