ばね振り子

ばね振り子

ばねの一端を固定し、他端におもりを付けたものをばね振り子といいます。

『ばね振り子の力学的エネルギー』項では、力学的エネルギー保存の法則に着目して、ばね振り子のおもりの各点での速さを求めました。
本項では、ばね振り子が単振動することに着目して、往復運動するおもりの周期を求めます。

水平ばね振り子

一端が固定され、他端に質量 m [kg] のおもりが付けられ、なめらかな水平面に置かれている、ばね定数 k [N/m] のばねを、自然長より A [m] 伸ばして（あるいは縮めて）静かに放した場合の運動を考えてみます。

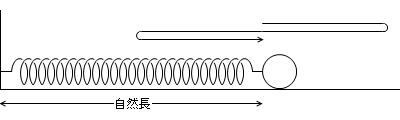
自然長の位置を原点Oとし、ばねが伸びる向きを変位 x [m] の正の向きとします。そうしますと、おもりにはたらく力（弾性力）F [N] はフックの法則より、

この式はまさに復元力の形になっているので、おもりは単振動をします。変位と力の向きが逆で、変位と力の大きさが比例しているからです。このような形の式が出てきたらすぐに「単振動」と連想してください。

おもりの加速度を a [m/s²] としますと、運動方程式より、

　　　　F = ma = - kx

　∴　　a = - \(\large{\frac{k}{m}}\)x

角振動数を ω [rad/s] とすると、単振動の加速度の式は

　　　　a = - ω²x

と表されるから、上式と比較すると、

　　　　\(\large{\frac{k}{m}}\) = ω²

であることがわかります。つまり、

　　　　ω = \(\sqrt{\large{\frac{k}{m}}}\)

さらに単振動の周期を T [s] とすると　T = \(\large{\frac{2\pi}{\omega}}\)　であるから、

となります。

この式より、おもりの質量 m が大きいほど、あるいは、ばね定数 k が小さいほど（すなわちばねがやわらかいほど）おもりの周期 T が大きい（ゆっくり振動する）と分かります。さらに振幅 A には無関係であると分かります。大きく引き伸ばしてからおもりを放したとしても振動の速さは変わらないということです。

鉛直ばね振り子

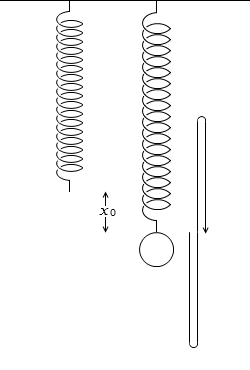ばね定数 k [N/m] のばね振り子を天井に固定し、他端に質量 m [kg] のおもりを付けて吊るしたとします。

重力加速度を g [m/s²] とし、おもりが自然長より x₀ [m] だけ伸びたところでつり合ったとすると、フックの法則より、

　　mg = kx₀　　……①

が成り立ちます。

鉛直下向きを x軸の正の方向、つり合いの位置を原点Oとします＊『鉛直ばね振り子の力学的エネルギー』においては、上向きを正とし、自然長の位置を原点としました。また、x₀ は d としました。
　閉じる。

つり合いの位置から鉛直方向にばねを伸ばして（あるいは縮めて）静かに放した場合の運動を考えてみます＊このとき、引き伸ばす長さ（振幅 A）が、x₀ より大きくても小さくても結果に変わりはありません。
　閉じる。

変位 x の位置をおもりが通過する瞬間には、k (x₀ + x) の上向きの弾性力と、下向きの重力 mg がおもりにはたらいているから、その合力 F [N] は

　　　　F = mg - k (x₀ + x)

です。この式に①式を代入すると、

　　　　F = kx₀ - kx₀ - kx = - kx

この式は上で説明した水平ばね振り子の式と同じであり、おもりは単振動をし、角振動数は

　　　　ω = \(\sqrt{\large{\frac{k}{m}}}\)

であり、周期は

となり、
おもりの質量 m が大きいほど、ばね定数 k が小さいほど、おもりの周期 T が大きく、振幅 A 、重力加速度 g には無関係であると分かります。

このように、自然長の位置ではなく、つり合いの位置を原点にとることによって水平ばね振り子と同じ式が得られることは『鉛直ばね振り子=水平ばね振り子』と『鉛直ばね振り子における中心について』で詳しく説明しました。

自然長の位置を原点にとると

もし自然長の位置を原点にとると、弾性力が kx で、重力が mg となりますので、合力 F は

　　　　F = - kx + mg

となり、①式を代入すると、

　　　　F = - kx + kx₀ = - k (x - x₀)

となります。

しかしこの式は、数学的に言えば　F = - kx　を x軸方向に x₀ だけ平行移動しただけのものであり、物理的に言えば x = x₀ の位置を中心として単振動するという意味の式であり、実質的には何も変わらないことになります。角振動数も周期も変わりません。

自然長の位置を原点にとってもつり合いの位置を原点にとっても実質的には同じということです。つり合いの位置を原点にとった方が式が簡単になります。