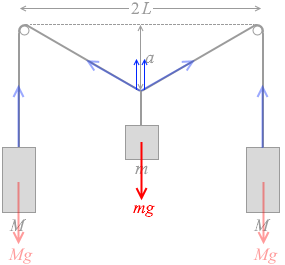
距離 2L だけ離れた小さな釘の間にひもが水平に張られており、両端には質量 M のおもりが同じ高さに取り付けられている。このひもの中点に質量 m のおもりをつり下げたところ、図3のように距離 a だけ下がったところでつり合った。a を L、m、M を用いて表わせ。ただし、ひもの質量は無視でき、ひもと釘の間の摩擦はないものとする。
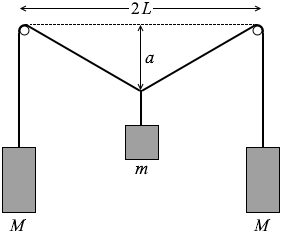
#センター07追試
距離 2L だけ離れた小さな釘の間にひもが水平に張られており、両端には質量 M のおもりが同じ高さに取り付けられている。このひもの中点に質量 m のおもりをつり下げたところ、図3のように距離 a だけ下がったところでつり合った。a を L、m、M を用いて表わせ。ただし、ひもの質量は無視でき、ひもと釘の間の摩擦はないものとする。

#センター07追試
重力加速度の大きさを g としますと、
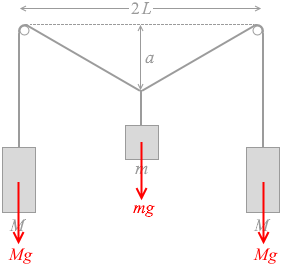 それぞれのおもりに Mg 、mg 、Mg の重力が掛かっています。
それぞれのおもりに Mg 、mg 、Mg の重力が掛かっています。
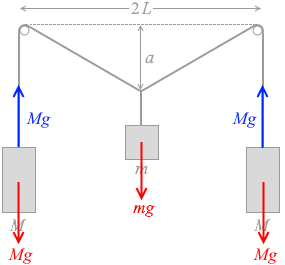 両端の質量 M のおもりについて考えますと、これらが静止しているのは、同じ Mg の力でひもに引っ張り上げられているからです。
両端の質量 M のおもりについて考えますと、これらが静止しているのは、同じ Mg の力でひもに引っ張り上げられているからです。
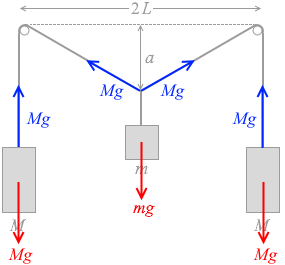 そして、1本でつながれたピンと張ったひもの張力はどの地点でも同じです。
そして、1本でつながれたピンと張ったひもの張力はどの地点でも同じです。
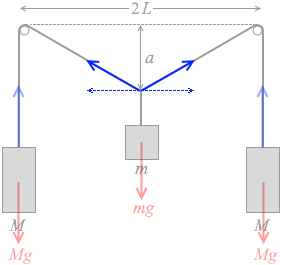 この張力は左右対称ですので、真ん中のおもりが左右に動いてしまうことはありません。つまり水平方向のつり合いはとれています。
この張力は左右対称ですので、真ん中のおもりが左右に動いてしまうことはありません。つまり水平方向のつり合いはとれています。
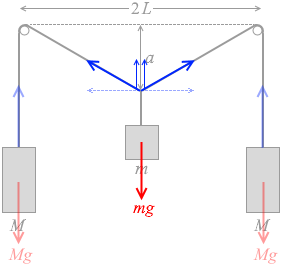 考えるべきは鉛直方向のつり合いです。mg の力の方が大きければ真ん中のおもりはズルズルと下に落ちていってしまいますし、逆なら上に持ち上がってしまいます。
考えるべきは鉛直方向のつり合いです。mg の力の方が大きければ真ん中のおもりはズルズルと下に落ちていってしまいますし、逆なら上に持ち上がってしまいます。
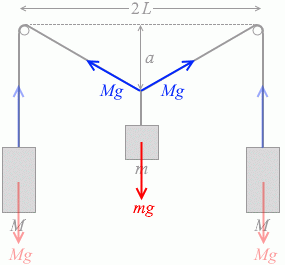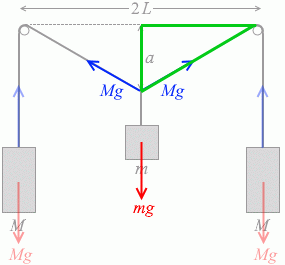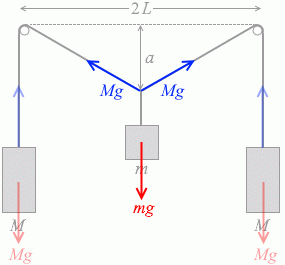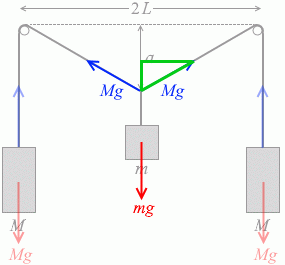 左図の2つの三角形が相似であることを使って Mg の鉛直成分を割り出します。
左図の2つの三角形が相似であることを使って Mg の鉛直成分を割り出します。
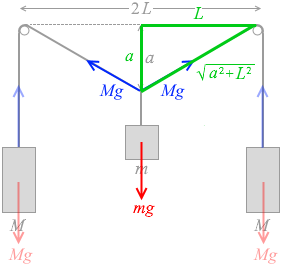 左図の三角形の斜辺の長さは三平方の定理(ピタゴラスの定理)より \(\sqrt{a^2+L^2}\) です。
左図の三角形の斜辺の長さは三平方の定理(ピタゴラスの定理)より \(\sqrt{a^2+L^2}\) です。
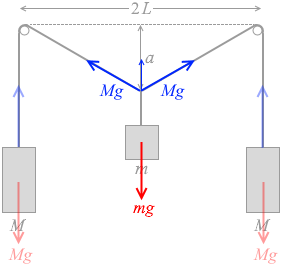 ですので、 Mg の鉛直成分は
ですので、 Mg の鉛直成分は
Mg × \(\large{\frac{a}{\sqrt{a^2+L^2}}}\)
です。
 この力2つと mg がつり合っているのですから、鉛直方向のつり合いの式は
この力2つと mg がつり合っているのですから、鉛直方向のつり合いの式は
2 × Mg × \(\large{\frac{a}{\sqrt{a^2+L^2}}}\) = mg
となり、
∴ 2 × M × \(\large{\frac{a}{\sqrt{a^2+L^2}}}\) = m
∴ 2Ma = m\(\sqrt{a^2+L^2}\)
∴ 22M2a2 = m2(a2 + L2)
∴ 22M2a2 - m2a2 = L2m2
∴ (22M2 - m2)a2 = L2m2 和と差の積の公式 A2-B2=(A-B)(A+B) より
∴ (2M - m)(2M + m)a2 = L2m2
∴ a2 = \(\large{\frac{L^2m^2}{(2M-m)(2M +m)}}\)
∴ a = \(\large{\frac{Lm}{\sqrt{(2M-m)(2M +m)}}}\)
と求められます。